Pares equivalentes
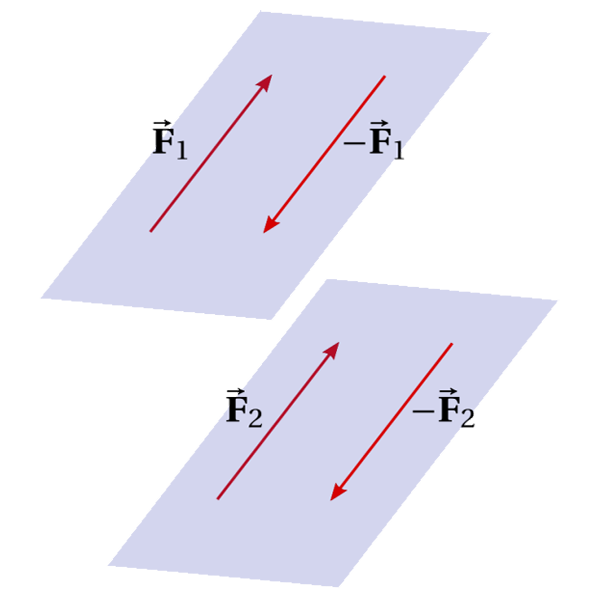
El par formado por las fuerzas F1→ y -F1→ definen un plano; El momento de par es perpendicular a dicho plano y por lo tanto, un par equivalente a este primer par debe producir un momento de par en la misma dirección. Así, el par equivalente, constituido por F2→ y -F2→ y debe estar contenido en el mismo plano o en un plano paralelo definido por las fuerzas del primer par.
En la siguiente figura, usando el principio de transmisibilidad y la ley del paralelogramo, es posible encontrar a partir de un par de fuerzas (F1→ y -F1→) un segundo par de fuerzas equivalente (F2→ y -F2→) (figura d) sobre el mismo plano, siguiendo el procedimiento que se menciona a continuación.
Primero se deslizan las fuerzas F1→ y -F1→ desde los puntos a y b hasta a' y b', respectivamente (figura b). Luego, utilizando la ley del paralelogramo se descompone la fuerza F1→ en el vector S→ que está dirigido a lo largo de la recta a'b y en el vector R→ a lo largo de la recta b'a' (figura c). De igual forma, se procede a descomponer -F1→ en los vectores -S→ y -R→ Como se observa en la figura c, R→ y -R→ son vectores que tienen la misma magnitud, están sobre la misma línea de acción y sus sentidos son opuestos. Por lo tanto, si estos vectores se deslizan hasta un punto de aplicación en común pueden cancelarse, quedando el par de fuerzas S→ y -S→ que corresponden al par F2→ y -F2→.

Teniendo presente qué pares equivalentes producen los mismos efectos sobre un determinado cuerpo rígido, no es necesario representar las fuerzas que forman un par, basta con dibujar un vector que posea la misma magnitud, dirección y sentido del momento τ→del par.
