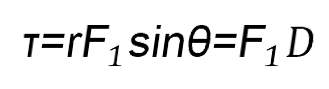Par de fuerzas

Las fuerzas F₁→ y F₂→ que actúan sobre el objeto, tienen la misma magnitud, líneas de acción paralelas y sentido contrario. Este tipo de fuerzas es conocido como un par o cupla, y se caracteriza porque su suma produce una fuerza neta igual a cero. Sin embargo, la adición de sus momentos de torsión alrededor de un punto O arbitrario es diferente de cero, y por lo tanto, el objeto sobre el que actúan tiende a rotar.

La siguiente figura representa un par de fuerza actuando sobre un cuerpo rígido. El momento producido por el par tiende a rotar el objeto.

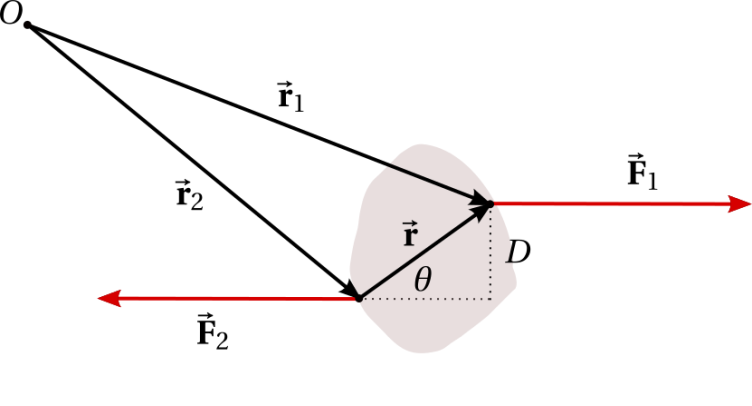
Los vectores r₁→ y r₂→ representan las posiciones de los puntos donde son aplicadas las fuerzas F₁→ y F₂→ respectivamente. El momento de torsión producido por este par alrededor del punto arbitrario O es:

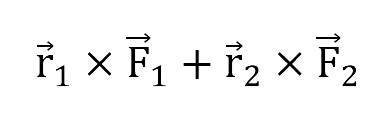
De igual forma, se observa que F₁→= -F₂→ y r→ = r₁→ - r₂→ por lo tanto, la anterior expresión se puede escribir como:

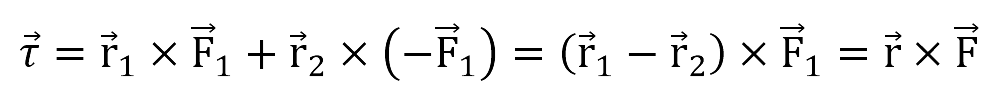
Donde el vector se conoce como momento del par y su resultado no depende del punto O escogido. Este vector es perpendicular al plano que contiene las dos fuerzas y su sentido está dado por la regla de la mano derecha. La magnitud del vector τ→ es: