Principio de transmisibilidad para el momento de una fuerza
¿Cómo se aplica el principio de transmisibilidad para el momento de una fuerza con respecto a un punto?. La punta del vector r se puede ubicar sobre cualquier punto de la línea de acción de F. Esto implica un momento de torsión igual para cualquiera de estos puntos, esto establece que F es un vector deslizante porque se ubica en cualquier punto de la línea de acción generando el mismo momento τ con relación al punto de giro O, ver la siguiente imagen:
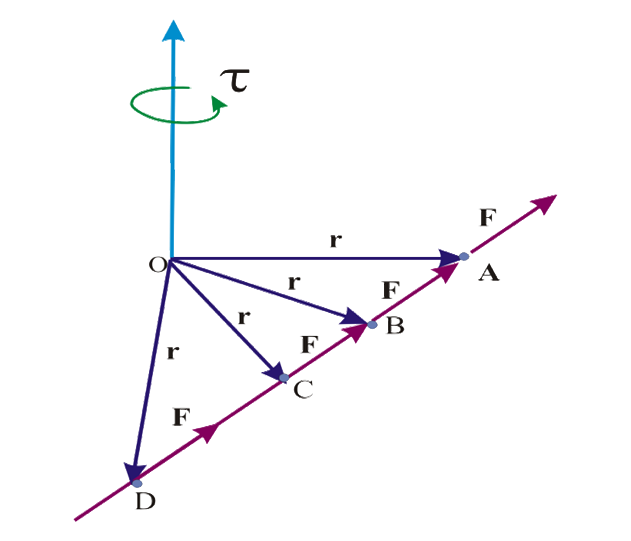
¿Cómo se calcula el momento de fuerza respecto a un punto para un sistema de fuerzas concurrentes F1, F2, F3, ..., FN?
Las fuerzas concurrentes se aplican sobre un mismo punto que lo denotamos con A, esto hace que las líneas de acción se corten en este. Para determinar el momento de fuerza con relación al punto O, primero se calcula la fuerza resultante o neta Fneta del sistema (método del polígono o adición de vectores de manera analítica). Después, se calcula el producto cruz utilizando esta fuerza resultante con la distancia del punto de giro O al punto A (vector de distancia r), donde se aplican las fuerzas, tal y como lo muestra el siguiente gráfico. A partir de este procedimiento, se deduce el momento de torsión general para las fuerzas concurrentes, esto corresponde al teorema de Varignon el cual se define como:
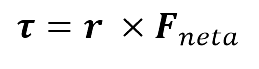
Un sistema de fuerzas concurrentes F1, F2, F3, ..., FN, en un punto A, el momento de torsión para el sistema en el punto O, corresponde al producto cruz entre la fuerza neta Fneta y la distancia r.
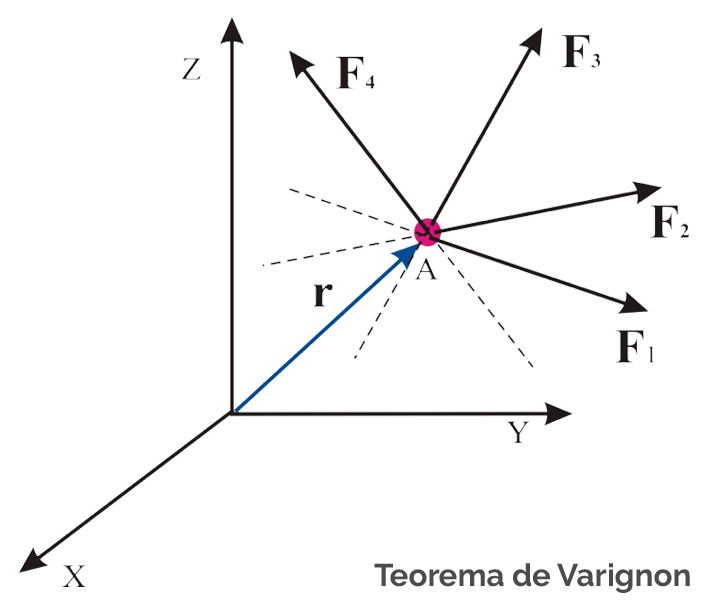
¿Cómo se calcula el momento de torsión en términos de sus componentes?
El momento τ se define estableciendo las coordenadas cartesianas de x, y, z para el vector posición r y el vector de fuerza F, tal que:

El cálculo se realiza de la misma manera como se explicó en el producto vectorial de dos vectores.
Ahora bien, suponiendo que hay una placa de acero rectangular de 4m x 6m que gira en el punto A con una fuerza FA=200N con una dirección respecto a la horizontal de φ=30° y utilizando el teorema de de Varignon, ¿cómo se calcularía el momento de torsión neto?.

La distancia entre el punto de giro y la línea de acción de la fuerza FA, corresponde entonces a:
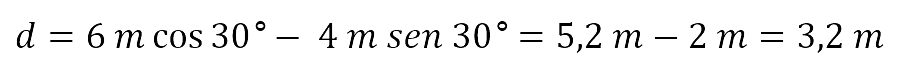
El momento de fuerza τA se puede calcular de dos formas. Una es el producto entre la fuerza y el valor de distancia, así:
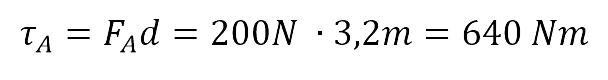
La otra opción es calcular las componentes rectangulares del vector fuerza y multiplicarlas por sus correspondientes distancias al punto de giro.
Valor de las componentes rectangulares:

Ahora se encuentra el valor de momento de fuerza para cada una:
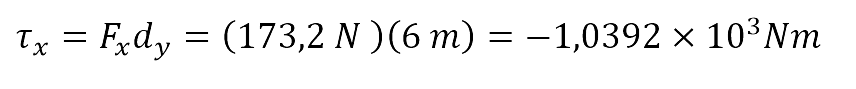
(negativo porque va en sentido de las manecillas del reloj)
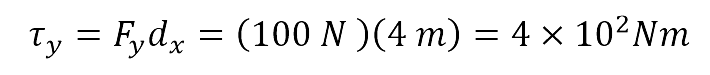
(positivo porque va en sentido contrario a las manecillas del reloj)
Por lo tanto, el momento total de fuerza es:
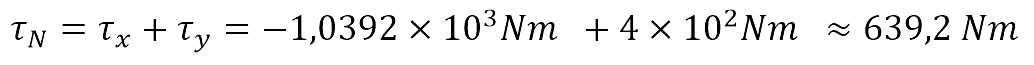
Entre los dos resultados se presenta una diferencia de 0.8 Nm.
