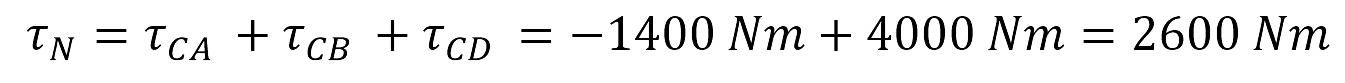Momento Vectorial
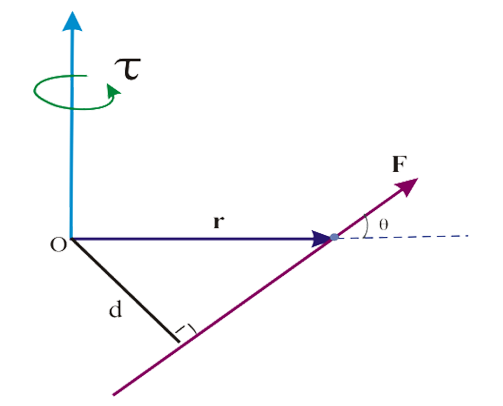
El efecto de rotación en un cuerpo rígido alrededor de un punto se define mediante el concepto de momento o torque. Esta cantidad física se define como la fuerza externa F que actúa sobre un cuerpo rígido a una distancia r del punto de giro O. Es importante mencionar que este punto no se encuentra sobre la línea acción de F, tal y como se muestra en la siguiente imagen:
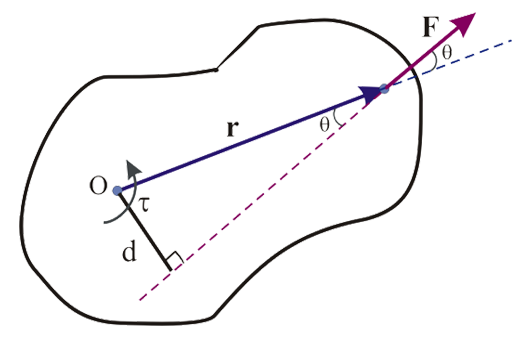
Por lo tanto, el momento de la fuerza F aplicada sobre el cuerpo rígido a un punto de giro O arbitrario en el espacio, se define como el producto:
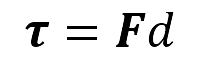
en donde corresponde a la distancia perpendicular entre O y la línea de acción de la fuerza F, así la magnitud del momento o torque de esta fuerza se define como:
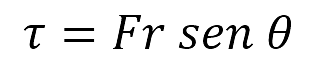
Revisando de nuevo el producto vectorial de dos vectores se encuentra que la magnitud del vector momento es:
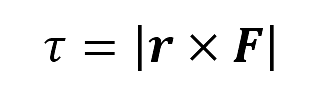
por consiguiente el vector está dado por:
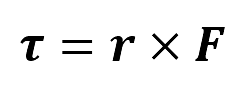
El momento vectorial o vector momento tiene como magnitud τ y su dirección concuerda con el eje de rotación sobre el punto O. La dirección y sentido del vector de momento τ se determina mediante la regla de la mano derecha, tal como se explicó para el producto vectorial de dos vectores, ver el siguiente gráfico.
Ahora, considere la siguiente placa metálica con tres orificios A, B y D. Las distancias al punto de giro C son: 28m, 40m y 15m respectivamente. Calcular los momentos de fuerza con relación al punto de giro C.

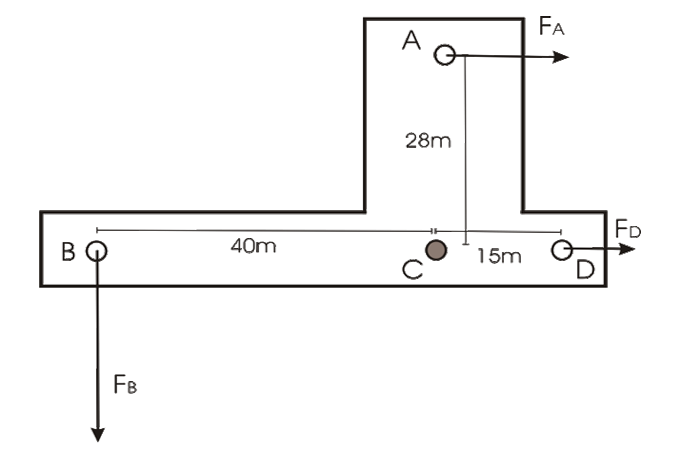
El momento τCA generado por la fuerza FA, es negativo porque su giro va en el sentido de las manecillas del reloj.
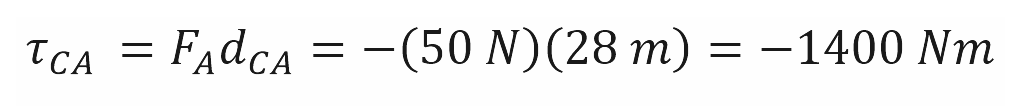
El momento τCB generado por la fuerza FB, es positiva porque su giro va en el sentido contrario de las manecillas del reloj.
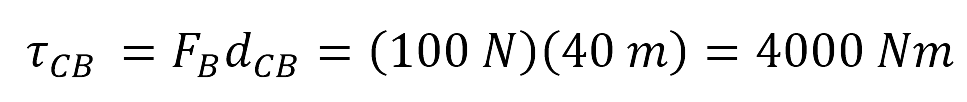
El momento τCD generado por la fuerza FD, es cero porque la dirección de la fuerza es paralela a la distancia CD→.
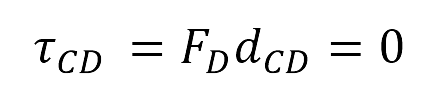
El momento neto o total τN del sistema corresponde a la suma de todos los momentos generados por las fuerzas presentes: