Producto vectorial entre dos vectores
En general el producto vectorial se subdivide en tres operaciones como son el producto de un escalar por un vector donde se obtiene un vector, el producto escalar o punto entre dos vectores del que resulta un escalar y finalmente el producto cruz entre dos vectores donde se obtiene un vector.
Dados dos vectores A y B, contenidos en un mismo plano, el producto cruz entre ellos se escribe como:

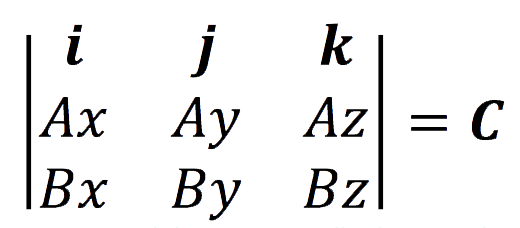
y de este modo se define el vector C, el cual es perpendicular tanta al vector A como al B.
La magnitud del vector C, es decir su longitud está dada por:

Esta corresponde al área del paralelogramo generado por los vectores A y B, tal como aparece en el siguiente gráfico:

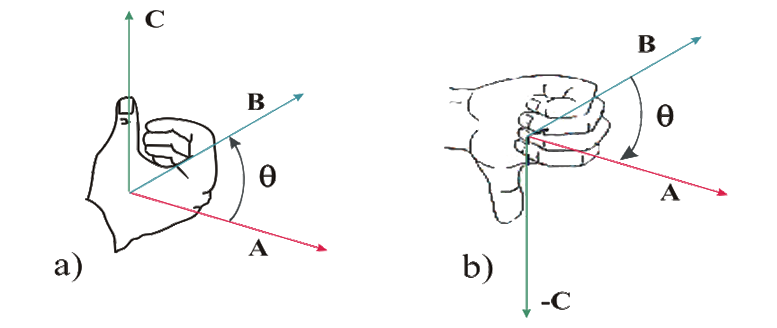
La orientación del vector C, depende de cómo se barre el ángulo entre los vectores A y B.

En la figura a), se observa que el ángulo se barre desde A hacia B, lo cual corresponde a AxB=C. En la figura b), el ángulo se barre desde B hacia A, esto hace que el producto cruz se determine como BXA=-C, en este caso C es paralelo al semieje de –y, por lo cual el sentido será contrario al anterior.
Así, se deduce que la multiplicación vectorial no es conmutativa sino anticonmutativa.

Esto implica que el orden de los factores en un producto cruz debe ser considerado con bastante cuidado.
En resumen el vector C, es el resultado del producto cruz entre dos vectores A y B. Es perpendicular a cada uno de estos vectores. Una regla muy útil para determinar la orientación perpendicular del vector C, es la de la mano derecha. Consiste en extender los dedos excepto el pulgar en dirección del vector A y se cierran hacia B, el pulgar indica la orientación perpendicular del vector C, tal como lo muestra la gráfica a). Si se realiza el producto BxA=-C, al utilizar esta regla el proceso es similar salvo que la mano se ubica sobre el vector B inicialmente y los dedos se cierran hacia el vector A, como se observa en la figura b).
Las propiedades del producto vectorial son:
- AxB = -BxA
- Ax(B+C) = AxB + AxC
- m(AxB) = (mA)xB = Ax(mB), con m escalar
- ixi = jxj = kxk = 0 y ixj = i, kxi = j
En el caso de un cuerpo rígido que gira alrededor de un eje AB con una velocidad angular. La velocidad lineal v en un punto de la trayectoria circular, está definido mediante el producto vectorial como: v = wxR , es decir el vector de velocidad angular perpendicular al radio R, por tanto se genera un vector velocidad tangencial a la trayectoria circular. El producto vectorial es importante, ya que se deben evaluar más adelante las condiciones de equilibrio de rotación, directamente es analizar los momentos de fuerza tal que el momento neto sea igual a cero.
Ejemplo
Ahora bien, dado dos vectores F1 y F2 con magnitudes de 4N y 7N, respectivamente. El ángulo θ entre F1 y F2 es de 30°, ¿cuál es la magnitud y orientación del vector resultante de F1xF2=F3? Para ello se tendrá en cuenta el siguiente gráfico.

El vector F3 es el resultante del producto. Mediante la regla de la mano derecha el pulgar de va hacia arriba, perpendicular al plano que contiene a los vectores F1 y F2. La orientación del vector F3, utilizando la regla de la mano derecha es hacia arriba perpendicular tanto a F1 como a F2. La magnitud de este vector es igual a:

Por otra parte, existen otras operaciones en el productor vectorial definidas como:
- Multiplicación por una constante k, tal que:
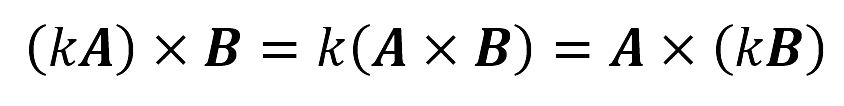
- Ley distributiva:
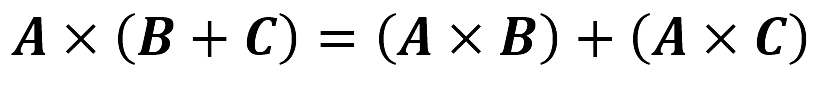
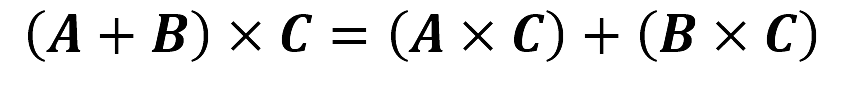
La ley asociativa no aplica para la multiplicación vectorial, es decir que:

Por otro lado, los productos vectoriales se pueden realizar en términos de los vectores unitarios i,j,k.
Sea el vector A = Axi+Ayj+Azk y B = Bxi→+Byj→+Bzk→ para encontrar el vector C, el método de solución se asocia con el cálculo de determinantes, así:

En general se tiene que:

Por ejemplo dados los vectores A = 2i+3j-4k y B = -i+2j-k, entonces el producto vectorial entre A y B está dado por:

Entonces el resultado del producto cruz entre A y B es:

