Fuerzas en tres dimensiones
En la siguiente figura se muestran tres vectores, los cuales tienen magnitudes y ángulos diferentes, ubicados en el primer, segundo y tercer cuadrante:
- F1 en el plano xy y forma un ángulo θ con el semieje x positivo.
- F2 en el plano –xy, forma un forma un ángulo β con el semieje y positivo y.
- F3 en el plano –x-y, formando un ángulo γ con el semieje –y.
La componente tanto en x como en y, de cada vector, será positiva o negativa dependiendo de la posición del ángulo que se escoja.

Cuadrante N1
En el primer cuadrante del plano cartesiano está el vector F1, y sus componentes son: F1x para la proyección en el semieje x y F1y para la proyección en el semieje y. Ahora bien, en la figura se observa un triángulo rectángulo (líneas punteadas) del cual se definen las componentes en función del seno y del coseno. Es decir que los catetos serían F1x y F1 y la hipotenusa corresponde a la magnitud del vector F1.

Por lo tanto, el determinar estas funciones en términos de los componentes resulta:
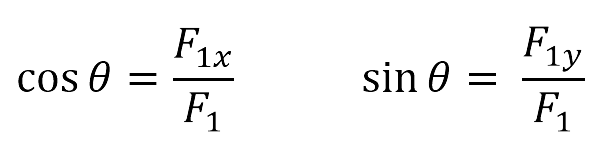
Despejando cada componente F1x y F1y, se obtiene para este caso en particular que:

Las componentes no se denotan en negrita porque es la magnitud del vector fuerza F1, el coseno y el seno son escalares.
A partir del triángulo rectángulo y del teorema de Pitágoras se deduce que la magnitud de F1 es:

y la dirección de F1 está relacionada con sus componentes mediante la siguiente expresión:

Cuadrante N 2
Realizando un proceso similar al anterior, se deducen a continuación las componentes para estos vectores, teniendo presente la ubicación del ángulo. En el vector F2, las componentes F2x proyección en x y F2y proyección en y, forman un triángulo rectángulo (líneas punteadas) cuyos catetos serían entonces F2x y F2y y la hipotenusa corresponde a la magnitud del vector F2.

Con respecto a lo anterior, se puede definir las funciones seno y coseno como:

Los componentes en este caso definen las funciones trigonométricas de esta manera, ya que corresponde al lado adyacente del triángulo rectángulo definiendo la función coseno, mientras es el lado opuesto al ángulo, relacionándose con la función seno.
Así, los componentes se determinan como:

La componente en x en negativa porque su proyección es sobre el semieje –x. La dirección negativa de F2 es porque el ángulo β se barre en el sentido de las manecillas del reloj, se definen entonces la magnitud y dirección por:

No se debe relacionar siempre el coseno con el eje x, ni el seno con el eje y, estas funciones las define la ubicación del ángulo.
Cuadrante N 3
El vector F3 ubicado en el tercer cuadrante del plano cartesiano, en donde la ubicación del ángulo define las funciones coseno y seno, debido a la formación de un triángulo rectángulo, de esta manera: los catetos son F3x y F3y y la hipotenusa corresponde a la magnitud del vector F3.


Ambas componentes F3y y F3x son negativas porque sus proyecciones están dadas sobre los semiejes y y x negativos, así:

La magnitud de F3 es siempre positiva debido a los cuadrados de sus componentes y la dirección es un ángulo positivo, indicando que se barre en el sentido contrario a las manecillas del reloj.

El vector de fuerza resultante se obtiene con el cálculo de las componentes de cada vector fuerza que actúa en el sistema.
