Métodos para la formación de células

Modelo de algoritmos binarios (análisis del flujo de producción)

Para el análisis de flujo de la producción, todas las partes en una familia deben requerir rutas similares. Mínimas modificaciones en la ruta estándar serán requeridas para nuevos miembros.

Se utiliza una medida de eficacia para evaluar la calidad de las soluciones obtenidas. Dicha medida penaliza tanto los movimientos intercelulares (contando el número de máquinas que deben visitar las partes fuera de la célula a las que están asignadas), como la falta de homogeneidad de las familias de partes (contando el número de veces que las partes no necesitan ser procesadas por todas la máquinas de la célula a la que están asignadas).

Se desarrolla de la siguiente manera:

  1. Clasificación de las máquinas: con base en las operaciones que pueden desarrollarse en cada una de ellas.
  2. Revisión de la lista de partes y de la información de producción.
  3. Recolección de datos: se recolectan los datos necesarios. Los objetivos definen la población de partes a ser analizadas. ¿Pueden todas las partes de piso ser incluidas en el estudio, o ser una muestra representativa del análisis? Desde que la población es definida, los datos necesarios mínimos en el análisis son el número de partes y la secuencia para todas estas. Los datos pueden ser obtenidos de las hojas de proceso.
  4. Clasificar las rutas de proceso: consiste en arreglar las partes dentro de grupos acordes a las similitudes de sus rutas de proceso. Para una cantidad grande de partes, un método manual acompaña este paso, es el codificar los datos coleccionados en el paso 1 dentro de archivos de computadoras.
  5. Carta PFA: los procesos usados para cada paquete son a continuación desplegados gráficamente.

  6. Análisis: este es el paso más subjetivo y difícil en el PFA, pero es el crucial en el procedimiento. Desde que se trazan los datos en la carta del PFA, grupos similares pueden ser identificados.

    Procedimiento para el análisis:

    1. Todas las máquinas o estaciones de trabajo en la planta son identificadas con un número.
    2. Se construye una gráfica PFA (partes vs máquinas) en la que se marcan las máquinas requeridas para el procesamiento de cada componente.
    3. Análisis de la gráfica PFA (matriz de incidencia) como identificación de partes con secuencias de proceso similares.
    4. Agrupamiento de las partes con secuencias idénticas o similares. Se reordena la gráfica.

    Los elementos de la matriz se denotan por:

    • I: estaciones de trabajo.
    • j: componentes.

    Los valores para Mij son:

    • Mij = 1 si al componente j le corresponde la estación de trabajo i.
    • Mij = 0 si al componente j no le corresponde la estación de trabajo i.

    Invariablemente, hay partes que no caen en grupos similares. Estas pueden ser analizadas para determinar si un proceso de secuencias revisado puede ser mejorado ajustándose dentro de uno de estos grupos. Si no, esta parte puede continuar procesándose en una distribución de proceso de tipo convencional.

    La debilidad del PFA es que los datos usados son tomados de las hojas de proceso. Las secuencias de los procesos de estas hojas han sido preparadas por diferentes planeadores de proceso, y las diferencias son reflejadas en las hojas de proceso. Las rutas pueden tener pasos no óptimos, ilógicos e innecesarios.

    El proceso que no se puede realizar se lleva a cabo fuera de la célula o FMS. Algunos procesos que se pueden dejar fuera de la célula o FMS, son los procesos que se realizan al final (inspección, ensamble, empaque, etc.).

    Análisis Grupo máquina – componente

    Está basado en el análisis de flujo de producción, se forma permutando renglones y columnas en la tabla de una matriz binara de ceros y unos.

    Sin embargo, la versión del Problema de Formación de Células de Manufactura que considera el orden de procesamiento para las partes, ha recibido mucha menor atención en la literatura. En este caso, los elementos de la matriz de incidencia máquinas-piezas son números enteros y representan el orden en el que las máquinas son utilizadas para producir las distintas partes. En este sentido, se hace mayor énfasis en el número de veces que una parte debe ser transportada de una célula de manufactura a otra y por tanto, esta versión del problema refleja de mejor manera la magnitud del manejo de materiales necesario dentro del sistema de manufactura. (Luna & Díaz, 2011).

    Análisis de agrupamiento por enlaces sencillos

    Se calculan coeficientes de similitud entre máquinas, se construye un árbol llamado dendograma. El coeficiente de similitud entre dos máquinas está definido como el cociente de las partes que visitan ambas máquinas y el número de partes que visitan una de las dos máquinas es:

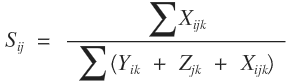
    Donde:

    Xijk = operación en la parte k realizada en las máquinas i y j.
    Yik = operación en la parte k realizada en la máquinas i.
    Zijk = operaciones en la parte k realizada en las máquinas j.
    S ijk = coeficiente de similitud entre la máquina i y j.

    Para construir un dendograma se deben seguir los siguientes pasos:

    1. Calcule los coeficientes de similitud para todas las posibles parejas de máquinas.
    2. Seleccione las dos máquinas con el coeficiente de similitud más alto.
    3. Baje el valor del coeficiente de similitud y forme una nueva célula de máquinas, incluyendo todas las máquinas con coeficiente de similitud no menor que el valor límite mínimo.
    4. Continúe con el paso 3 hasta que todas las máquinas estén agrupadas dentro de una célula sencilla.