El Teorema de Tchebysheff
El teorema es válido para cualquier variable aleatoria. Gráficamente para distribuciones sesgadas o simétricas, siempre y cuando k≥1. En la tabla se encuentran los intervalos definidos mediante la media \widetilde { x } y la desviación estándar S. También, se especifican algunos valores para k, los cuales permiten determinar el porcentaje de mediciones por intervalo.
| k | 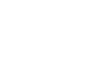 |
Intervalo |
Proporción de mediciones |
| 1 | 0 | 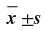 |
0 |
| 2 | 3/4 | 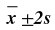 |
75% |
| 3 | 8/9 | 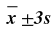 |
 89% 89% |
| 4 | 15/16 | 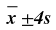 |
 94% 94% |
Tabla 1. Algunos valores numéricos para k . Con estos se calculan las proporciones de las mediciones mediante: 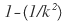 , se especifican los intervalos que acotan las regiones dentro de la distribución de frecuencias y se asigna su correspondiente porcentaje con relación a la cantidad de datos.
, se especifican los intervalos que acotan las regiones dentro de la distribución de frecuencias y se asigna su correspondiente porcentaje con relación a la cantidad de datos.
Cuando k=0 no es del todo útil, pero los demás valores para esta constante ofrecen información importante frente al porcentaje o proporción de las mediciones por los intervalos dados. No solo k toma valores enteros, por ejemplo, si k =2,5 entonces localiza dentro del respectivo intervalo un porcentaje en la medición del 84% de los datos. En el cálculo de probabilidades este teorema proporciona información valiosa para el análisis de las distribuciones de probabilidad.
