Transformación de la ecuación de longitud de un arco

Sea la ecuación:

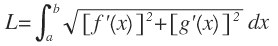
Al transformarla de coordenadas rectángulares a polares, se deben tener en cuenta las ecuaciones paramétricas:

x = F(θ)cosθ y = F(θ)senθ

Por lo tanto, si F’ es continua al remplazar tendremos:

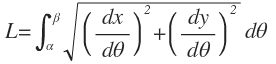
Donde:

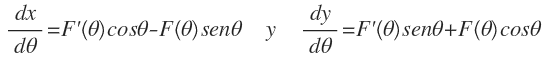
Por lo cual, se puede decir que:

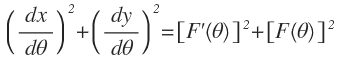
Donde F’(θ)=dr/dθ, y F(θ)=r, y al remplazar se obtiene:

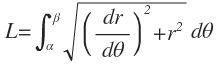
Para la longitud del arco en coordenadas polares.

Ejemplo 1

Calcular la longitud del arco de la cardioide r = 2(1+cosθ).

Solución

Como r = 2(1+cosθ), entonces: dr/dθ = -2 senθ. Integrando entre 0 y π, y viendo la simetría nos queda:

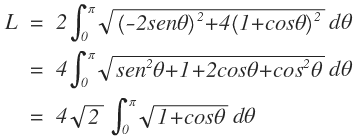
Para evaluar la integral usamos la identidad trigonométrica: cos² (θ/2)=1/2 (1+cosθ), donde siendo 0≤θ≤π, nos queda: 0≤θ/2≤π/2, y como cos(θ/2)≥0, entonces:

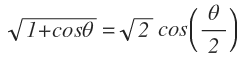
Y remplazando en la integral nos queda:

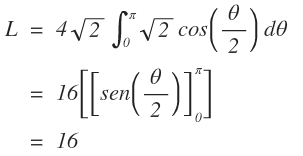
La representación gráfica de la cardioide r=2(1+cosθ), es:

Figura 1. Gráfica del ejemplo

Ejemplo 2

Calcular el área de la región limitada por la cardioide:: r=2+2cosθ.

Solución

Como se muestra en la figura 2, la gráfica es simétrica respecto al eje polar y los límites de θ son: 0 y π. Entonces, nos queda:

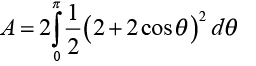
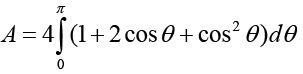
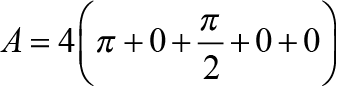
=6π unidades cuadradas.

Figura 2. Gráfica del ejemplo