Teoremas 10, 11 y 12

Teorema 10

Sea c cualquier constante diferente a cero.

1. Si la serie 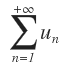es convergente y su suma es S, entonces la serie también es convergente y su suma es cS.

2. Si la serie 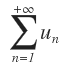es divergente, entonces la serie también es divergente.

Teorema 11

Si 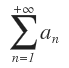y 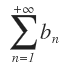son series infinitas convergentes cuyas sumas son S y T, respectivamente, entonces:

1. Serie convergente y su suma es S + T

   

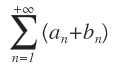
2. Serie convergente y su suma es S - T

   

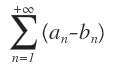
Si (1) es convergente y la serie (2) es divergente, entonces la serie (3) es divergente.

(1)
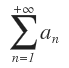(2)
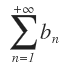(3)

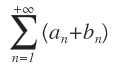Teorema 12

Si 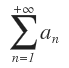y 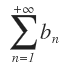son dos series infinitas que difieren únicamente en sus primeros términos (es decir que: a_k = b_k si k > m), entonces las dos series son convergentes o ambas son divergentes.