Teorema 1. Definición del límite de una sucesión

Siendo L un número real, se dice que L es límite de una sucesión {a_n}, y se denota:

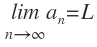
Si para cada ϵ > 0 existe un M > 0 tal que | a _n - L | < ϵ siempre que n > M. Las sucesiones que tienen límite se llaman convergentes y las demás se llaman divergentes.

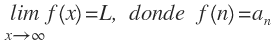
Ejemplo

Hallar el límite de la sucesión cuyo término general es:

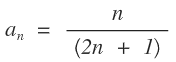
Procediendo de acuerdo con el teorema anterior, tenemos:

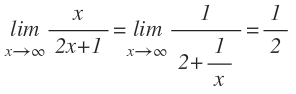
Así, tenemos que:

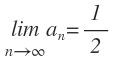
Siendo n un número entero positivo.