Ejemplo
El tercer polinomio de Maclaurin para sen x, es: P3(x) = x - x3/3!.
A partir de esta información, use el teorema de Taylor para aproximar por: P3(0,1), luego el valor de sen(0,1) .
¿Cuál es la precisión de esta aproximación?
Solución
Según el teorema de Taylor, tenemos que:

Donde 0 < z < 0,1, por lo tanto:
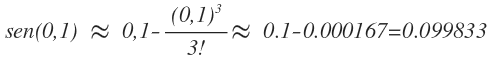
De f 4(z) = sen z se tiene que el error |R3(0,1)| admite la siguiente acotación:
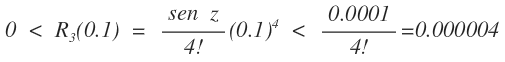
Lo que implica que:
0.099833 < sen(0.1) < 0.099833 + R3(x) < 0.099833 + 0.000004
Por lo cual, nos queda:
0.099833 < sen(0.1) < 0.099837
Demostrando lo solicitado.
