Criterio de la Raíz
Teorema 21. El criterio de la raíz
Sea ∑an una serie con términos no nulos.
- ∑an es convergente absolutamente si
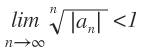
- ∑an es divergente si
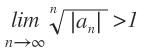 o
o 
- El criterio del cociente no es concluyente si
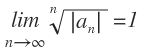
Ejemplo
Determinar si la serie 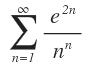 es convergente o divergente..
es convergente o divergente..
Solución
Aplicando el criterio de la raíz, tenemos que:

Debido a que el límite es menor que uno, se concluye que la serie es absolutamente convergente.
