Convergencia absoluta y condicional
Cuando una serie tiene términos positivos y negativos, pero no es alternada se requiere otro criterio para determinar su convergencia o divergencia. Para entender esta situación veamos el teorema 19:
Teorema 19. Convergencia absoluta y condicional
Si la serie ∑|an| es convergente, la serie ∑an también es convergente, y entonces:
- ∑an es absolutamente convergente si ∑|an| converge.
- ∑an es condicionalmente convergente si ∑an converge, pero ∑|an| diverge.
Para entender lo expuesto en el teorema analicemos los siguientes ejemplos:
Ejemplo
Determine si la serie
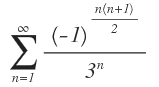
Es absolutamente convergente, condicionalmente convergente o divergente.
Solución
Vemos que esta serie no es alternada, pero también observamos que
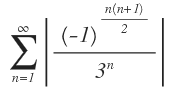
La podemos comparar con la serie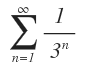 
, la cual es una serie geométrica convergente. De acuerdo con lo expuesto y con base en el teorema 19, la serie
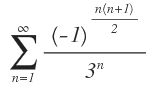
Es absolutamente convergente (y por ende convergente).
Ejemplo
Determine si la serie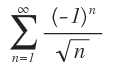 
es absoluta o condicionalmente convergente, o absoluta o condicionalmente divergente.
Solución
De acuerdo con el criterio de series alternadas (pues, en efecto, es alternada) esta serie es convergente, además siendo p-serie, nos queda:
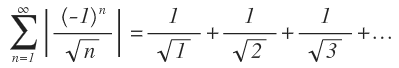
Que es divergente, luego la serie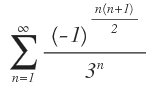 
es condicionalmente divergente.