Resto de una serie alternada
Teorema 18. Resto de una serie alternada
Si una serie alternada convergente satisface la condición an + 1 ≤ an, el valor absoluto del resto (Rn) al aproximar la suma S por (S) es menor o igual que el primer término desechado. Es decir:
Ejemplo. Cálculo aproximado de una serie alternada o alternante
Aproximar la suma de la siguiente serie por medio de sus primeros términos.
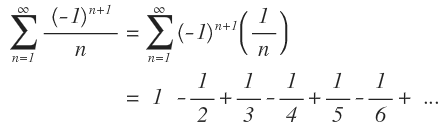
Solución
La serie converge de acuerdo con el criterio de serie alternada o alternante porque:
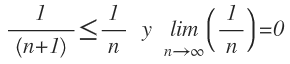
La suma de los primeros seis términos es:
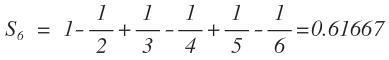
Y por el teorema del resto de la serie alternada o alternante, tenemos:
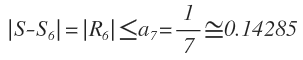
Así, la suma de S está entre 0.61667 – 0.14285 y 0.61667 + 0.14285, concluyendo que:
0.47382≤S≤0.75952
