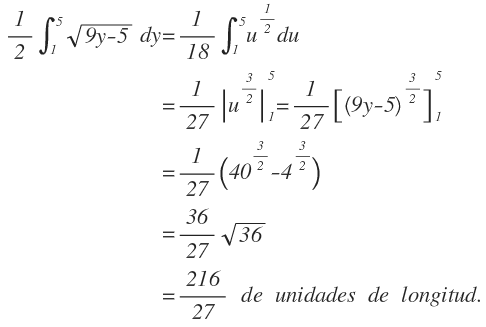Longitud de un arco

Ejemplo 1

Calcular la longitud del arco de la curva y = 1/6x³ + 1/(2x) en el intervalo [1/2, 2].

Para resolver este ejercicio debemos obtener la derivada de f(x), entonces:

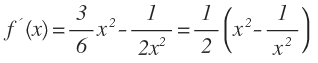
Luego tenemos que la longitud del arco será:

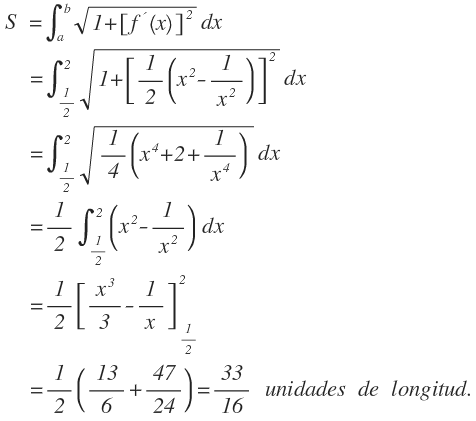
Figura 1. Arco del ejemplo

Ejemplo 2

Calcular la longitud del arco de la función (y-1)³ = x² en el intervalo [0, 8], tal como se ve en la figura 2:

Figura 2. Representación del ejemplo

Primero debemos despejar x en términos de y, es decir: x = ±(y - 1)^1/2.

Tomando únicamente el valor positivo para x , obtenemos la derivada, así: dy/dx = 3/2 (y - 1) ^1/2 y vemos que para el intervalo [0, 8] en tenemos el intervalo [1, 5] en y , por lo que la longitud del arco estará dada por:

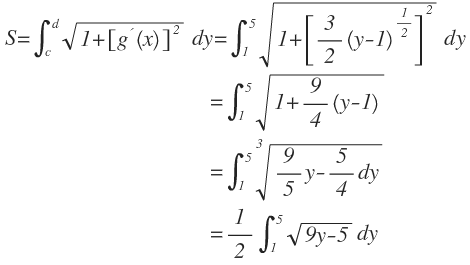
Cambiando de variable, tenemos:

u = 9y - 5, du = 9dy, de donde: dy = du/9

Reemplazando en la integral, entonces: