Volumen de sólidos usando discos o rebanado
Si r se mantiene constante y varía la altura h, entonces: ΔV = π r2Δh, que si estamos rotando sobre el eje x se cambia por: ΔV = π r2Δx .
Figura 1. Volumen acorde a pequeñas áreas.
Tomada de: Larson, Hostetler y Edwards (2006).
Si aproximamos con n discos de ancho Δx, y radio r(Xi), se obtiene que el volumen estará dado por:
Volumen del Sólido
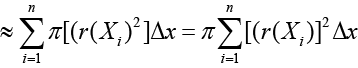
Por tanto, si Δx → 0 (n → ∞), entonces tendremos:
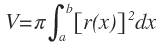
Si hacemos que r(x) = R(x), podemos establecer una ecuación para el método de discos, así:
| Fórmula de volumen | Elemento representativo | Nueva fórmula de integración |
 |
 |
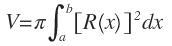 |
