Teorema 9. Momentos y centro de masa de una región plana

Sean f y g continuas con f(x)≥g(x) en [a, b] y consideremos la lamina de densidad uniforme ρ acotada por las gráficas de y=f(x), y=g(x) y a≤x≤b.

1. Los momentos respecto al eje x y al eje y son:

   

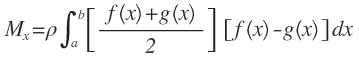
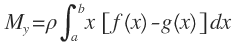
2. El centro de masa (xy es: (x̄ + ȳ) viene dado por x̄ = M_y/m y ȳ = M_x/m, donde:

   

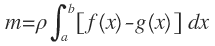
   Es la masa de la lámina.

Ejemplo

Hallar el centro de masa de la lámina de densidad uniforme ρ acotada por la gráfica de f(x)=4 - x² y el eje x.

Solución

Como el eje está en el eje de simetría, sabemos que x = 0. Además, la masa de la lámina es:

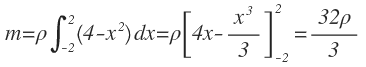
Para calcular el momento respecto al eje x, de acuerdo con la figura 1, entonces el rectángulo es:

Figura 1. Rectángulo del ejemplo.

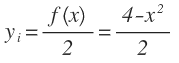
Entonces la masa es:

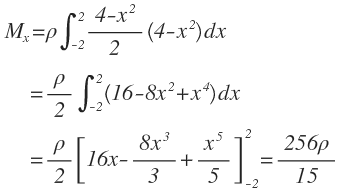
Entonces:

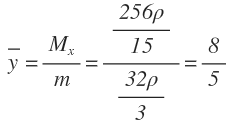
De tal manera que el centro de masa (o punto de equilibrio) es (0, 8/5), lo cual se refleja en la figura 2:

Figura 2. Centro de masa del ejemplo.