Nueve casos de integrales trigonométricas

Caso 1

(i)

(ii)

Donde n es un número entero positivo impar.

(i) Factor:

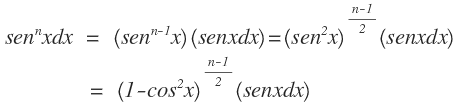
(ii) Factor:

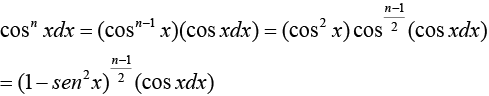
Ejemplo

Calcular la integral

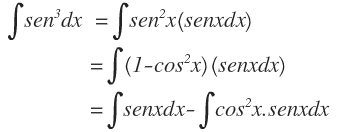
La primera integral se calcula en forma directa —además de ser conocida ya— mientras que la segunda integral la calcularemos por sustitución, así:

Sea u=cosx, entonces du=senxdx, por lo tanto al reemplazar tendremos:

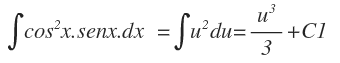
Y finalmente tendremos como resultado:

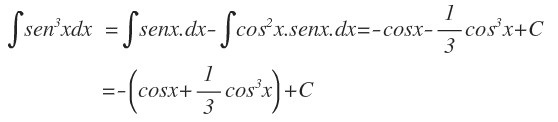
Caso 2

, donde al menos uno de los exponentes es un número entero positivo impar. Utilizando un método de solución semejante al anterior tendremos:

(i) Si n es impar, entonces:

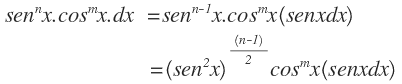
(ii) Si m es impar, entonces:

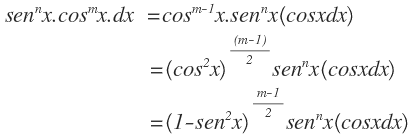
Ejemplo

Calcular la integral

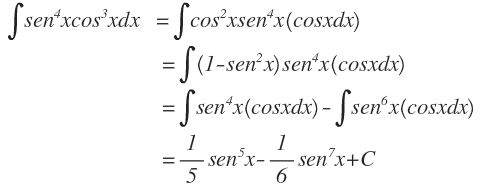
Caso 3

No se pueden aplicar los mismos métodos de solución cuando los exponentes no son enteros impares, sino que son enteros pares. Para ese caso tenemos:

(i)

(ii)

(iii)

Donde m y n son enteros positivos pares.

(i) Factor:

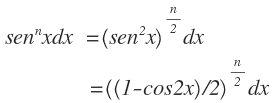
(ii) Factor:

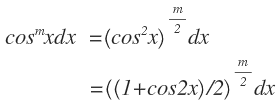
(iii) Factor:

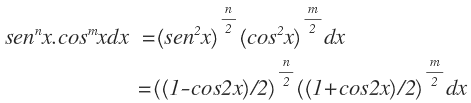
Ejemplo

A continuación vienen los casos restantes, los cuales involucran las demás funciones trigonométricas y sus combinaciones de orden mayor o igual a dos.

Caso 4

(i)

(i)

Donde n es un número entero positivo.

(i) Factor:

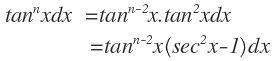
(ii) Factor:

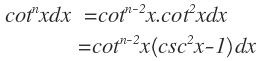
Ejemplo

Calcular las siguientes integrales:

(i)

(ii)

Caso 5

(i)

(i)

Donde n es un número entero positivo par.

(i) Factor:

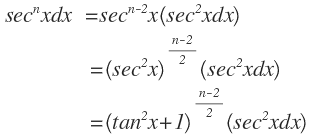
(ii) Factor:

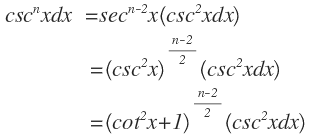
Ejemplo

Calcular la integral :

Caso 6

(i)

(i)

Donde m es un número entero positivo par.

(i) Factor:

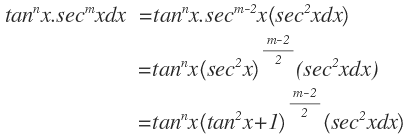
(ii) Factor:

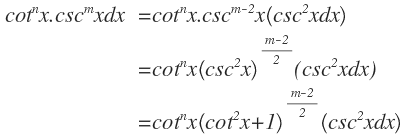
Ejemplo

Calcular la integral :

Se procede de acuerdo con lo mostrado en el caso 6, sección (i).

Caso 7

(i)

(i)

Donde n es un número entero positivo impar.

(i) Factor:

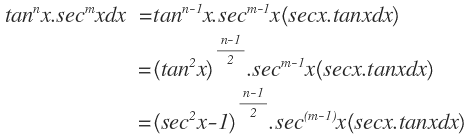
(ii) Factor:

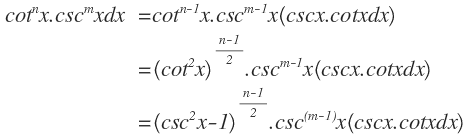
Ejemplo

Calcular la integral :

Caso 8

(i)

(i)

Donde n es un número entero positivo impar.

(i) Factor. Se debe aplicar integración por partes, así:

Considere

(ii) Factor. Aplicando integración por partes, se tiene:

Considere y

Ejemplo

Calcular la integral :

Sea y , entonces podemos integrar por partes, así:

Organizando, nos queda:

Nuevamente aplicando integración por partes a la última integral, sea y , entonces y , por lo tanto:

Pasando esta integral al otro lado y despejando, obtenemos:

Por lo que el resultado final es la integral∶

Caso 9

(i)

(ii)

Donde n es un número entero positivo par y m es un número entero positivo impar.

(i) Factor:

Se expresa el integrando en potencias impares de la secante o cosecante y se sigue el proceso del caso 8.

Ejemplo

Calcular la integral :

De aquí en adelante se evalúa según el ejemplo del caso 8.