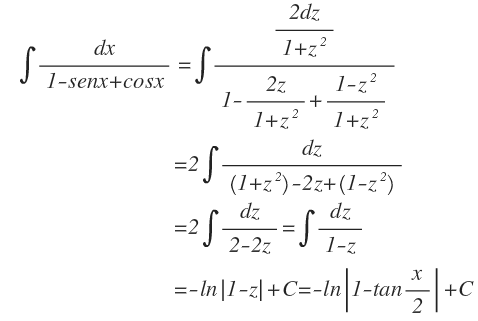Obtención o expansión en fracciones parciales

Sea:

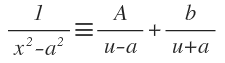
Si multiplicamos por (u - a)(u + a), obtenemos:

Donde al igualar los coeficientes, obtenemos: A + B = 0 y Aa - Ba = 1. Solucionando estas dos ecuaciones para A y B, obtendremos que: A = 1/(2a) y B = - 1/(2a).

De esta manera, la expansión en fracciones parciales queda de la siguiente manera:

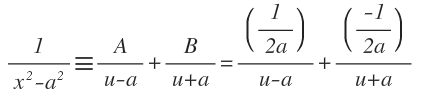
Ejemplo

Calcular la integral:

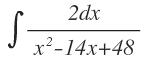
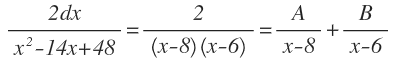
Entonces al separar las variables nos queda:

2=A(x-6)+B(x-8)=x(A+B)-6A-8B

De donde salen como ecuaciones: A + B = 0 y -(6A + 8B) = 2.

Solucionando este sistema de ecuaciones, primero: A = -B y reemplazando en la otra ecuación, nos queda:

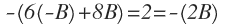
Es decir: B = -1, y por lo tanto: A = 1

Ahora, para solucionar la integral aplicamos la expansión en fracciones obtenida, así:

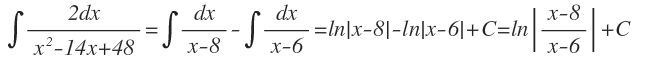
Teorema 1

Si z = tan x/2, entonces:

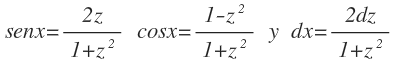
Ejemplo

Calcular la integral