Teoremas 11, 12 y 13
Teorema 11. Definición de integral definida
Sea f una función definida en el intervalo cerrado [a, b] y existe el límite:

Entonces f es integrable en [a, b] y el límite anterior lo podemos escribir o denotar como:
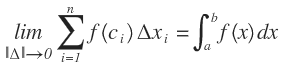
Que no es otra cosa que la integral definida de f(x) entre a y b, donde a es el límite inferior y b es el límite superior.
Teorema 12
Si una función f es continua en el intervalo [a, b], entonces f es integrable en [a, b].
Teorema 13
Si f es continua y no negativa en el intervalo cerrado [a, b], el área de la región limitada por la gráfica de f, el eje x y las rectas verticales x=a y x=b viene dada por:
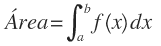
Ejemplo de aplicación de los Teoremas 11 y 12
Calcular la integral definida ∫02 4x dx
Solución
La función f(x) = 4x es integrable en el intervalo [0, 2], por ser continua. Si usamos cualquier partición cuya norma tienda a cero, podemos calcular el límite respectivo. Si definimos ∆ dividiendo el intervalo [0, 2] en n subintervalos de igual longitud, tenemos:
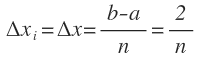
Eligiendo como ci el punto terminal derecho de cada subintervalo, tenemos:
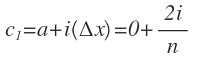
De donde definimos la integral como:
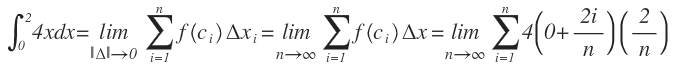
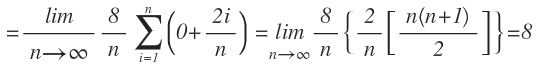
Ejemplo de aplicación Teorema 13
Considérese la región acotada por la curva f(x) = 4x - x2 y el eje de las x. Al ser f continua y no negativa en [0, 4] entonces el área de la región es:
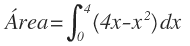
Área
Recuerda que un área es un concepto métrico que permite asignar una medida a la extensión de una superficie, expresada en matemáticas unidades de medida denominadas unidades de superficie. El área es un concepto métrico que requiere la especificación de una medida de longitud. Para superficies planas, el concepto es más intuitivo. Cualquier superficie plana de lados rectos —es decir, cualquier polígono— puede triangularse, y se puede calcular su área como suma de las áreas de los triángulos en que se descompone. Ocasionalmente se usa el término «área» como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área) (Wikipedia, 2017).
