Cálculo del área de una región plana

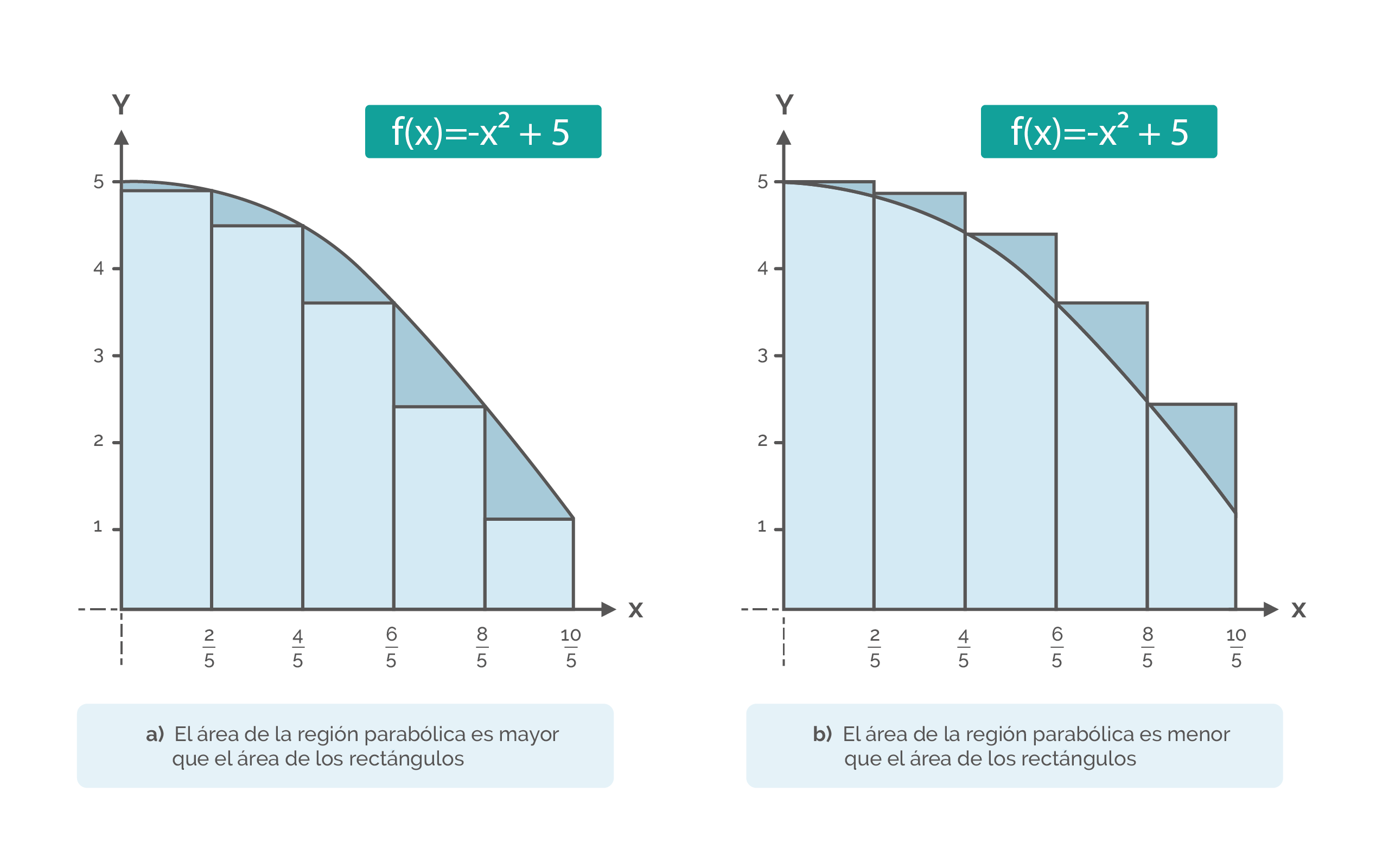
Con base en las figuras a y b, encuentre dos aproximaciones del área de la región acotada por la gráfica de: f(x) = x² + 5, y el eje x, entre x = 0 y x = 2.

Solución

1. Veamos en la gráfica «a» que los puntos están en 2/5i, donde i= 1, 2, 3, 4 y 5. El ancho de cada rectángulo es 2/3, y el alto puede calcularse evaluando a f en el punto terminal derecho de cada intervalo. Estos intervalos son:

   

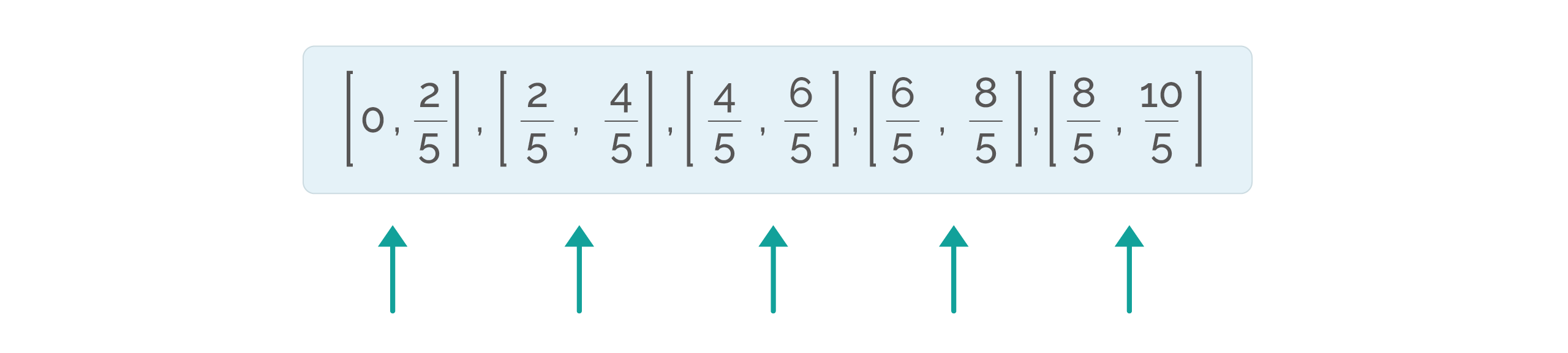
   Evaluar a f en los puntos terminales de la derecha de estos intervalos. Utilizando la notación sigma, la suma de las áreas de los cinco rectángulos es:

   

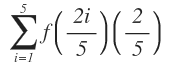
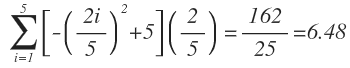
   Como cada rectángulo está dentro de la región parabólica, se concluye que el área de la región es mayor que 6.48.

2. En la gráfica «b» los puntos terminales de la izquierda en los intervalos son 2/5 (i-1), donde nuevamente i= 1, 2, 3, 4, y 5. En este caso, el ancho de cada rectángulo es 2/5 y el alto se obtiene evaluando a f en el punto terminal izquierdo de cada intervalo:

   

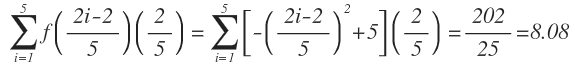
   Como la región parabólica está contenida en la unión de los cinco rectángulos, se concluye que su área es menor a 8.08.

   Ahora, combinando los dos resultados, podemos decir que: 6.48 < el área de la región < 8.08.

   Es claro que entre más rectángulos se tomen como referencia, mayor será la aproximación al área de la región.

   De acuerdo con lo anterior, podemos decir que la suma de los rectángulos inscritos se llama la suma inferior y la de los rectángulos circunscritos se llama la suma superior. Si llamamos la altura de los inscritos f(m_i), y la de los circunscritos f(M_i), entonces:

   Área del rectángulo inscrito = f(m_i)Δx ≤ f(M_i)Δx = área del rectángulo circunscrito.

   Suma inferior
   = s(n)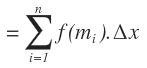

   

   Área de rectángulos inscritos.

   Suma superior
   = S(n)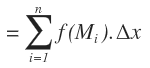

   

   Área de rectángulos circunscritos.