La Antiderivación
La antiderivación o antidiferenciación es el proceso por el cual se determina el conjunto de todas las antiderivadas de una función dada. Es denotada por el símbolo ʃ y se escribe:
ʃ f(dx) = F(x) + C (1)
Donde F´(x) = f(x), y
d (F(x)) = f(x)dx (2)
A partir de 1 y 2 podemos expresar esta relación de la forma:
∫ d(F(x))=F(x)+C (3)
Esta expresión nos deja ver que cuando se antideriva la diferencial de una función se obtiene la función más una constante arbitraria, mostrando que la diferencial y la antiderivada son inversas y que, por tanto, la antiderivación es la operación para obtener o determinar el conjunto de todas las funciones que tiene una derivada dada.
Esta operación también recibe el nombre de integración indefinida y se representa por la expresión general:
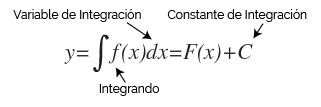
Donde a partir de ahora denotaremos que F es una primitiva de f en un intervalo.
En este punto podemos ver cómo se relacionan la derivada y la integral, únicamente se requiere transformar la forma de presentación de las ecuaciones, lo cual nos muestra con claridad la naturaleza inversa de la integración y la derivación.
Si retomamos la ecuación 4 y sustituimos a f por F´, entonces tenemos:
∫ F'(x)dx=F(x) + C
Y si además:
∫ f(x)dx=F(x) + C
Entonces podemos expresar esta relación como:
d/dx ∫ f(x)dx = F(x) + C (5)
Esto demuestra el proceso de la inversa, además de permitirnos obtener las fórmulas de integración directamente de las fórmulas de derivación.
