Ejemplo estimación por intervalos para la varianza

Los siguientes son los pesos, en decagramos, de 10 paquetes de semillas de pasto distribuidos por cierta compañía: 46.4, 46.1, 45.8, 47.0, 46.1, 45.9, 45.8, 46.9, 45.2 y 46. Encuentre un intervalo de confianza de 95% para la varianza de todos los paquetes de semillas de pasto que distribuye esta compañía; suponga una población normal. (Walpole, 307).

Solución:

Primero se calcula la desviación estándar de la muestra:

al elevar este resultado al cuadrado, se obtiene la varianza de la muestra s²= 0.286.

Para obtener un intervalo de confianza de 95% se elige un α= 0.05. Después, con el uso de la tabla con 9 grados de libertad, se obtienen los valores de X².

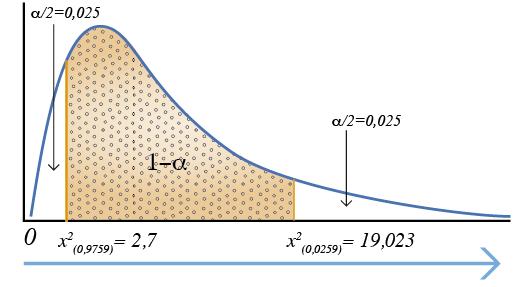
Se puede observar en la gráfica anterior, que el valor de X2 corre en forma normal, esto es de izquierda a derecha.

Por lo tanto, el intervalo de confianza de 95% para la varianza es:

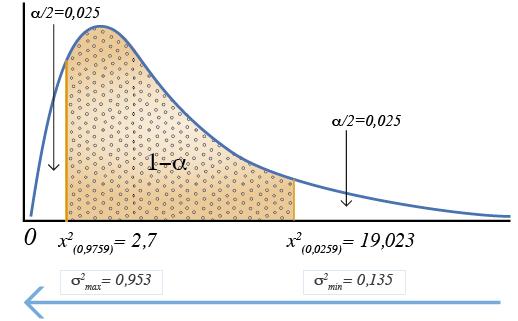
Se observa que la varianza corre en sentido contrario, pero esto es sólo en la gráfica. La interpretación quedaría similar a los temas anteriores referentes a estimación. Con un nivel de confianza del 95% se sabe que la varianza de la población de los pesos de los paquetes de semillas de pasto está entre 0.135 y 0.935 decagramos al cuadrado.