Estimación de la media para muestras pequeñas
En la mayoría de las situaciones no es fácil acceder a la desviación estándar poblacional, motivo por el cual si se toma evidencia y se calcula el promedio y la desviación estándar muestral (s) de una población que se comporte de forma aproximadamente normal, entonces la variable aleatoria:
Tiene una distribución t de student con n-1 grados de libertad.
La apariencia general de la distribución t es similar a la de la distribución normal estándar: ambas son simétricas y unimodales, y el valor máximo de la ordenada se alcanza en la media μ=0.Sin embargo, la distribución t tiene colas más amplias que la normal, esto es, la probabilidad de las colas es mayor que en la distribución normal. A medida que el número de grados de libertad tiende a infinito, la forma límite de la distribución t es la distribución normal estándar.
De manera similar que con la normal, se puede construir un intervalo de confianza así:
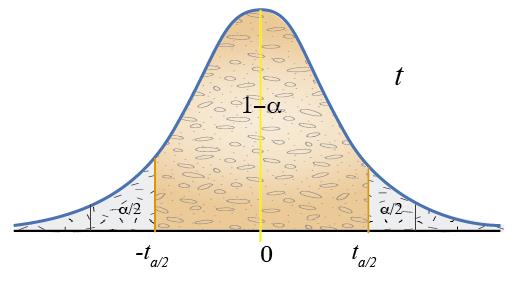
Reemplazando el estadístico:
Despejando µ:
