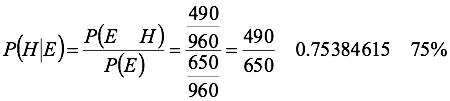Dos sucesos son independientes si la probabilidad de presentación de uno no se ve afectada por el otro. Hay que anotar que el enlace en este tipo de sucesos es “i”, es decir, que se den el uno y el otro. También hay que tener en cuenta que en estos experimentos, el muestreo se hace con reposición. El axioma es:
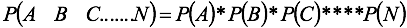
Si se tiene un mazo de 52 cartas y se extraen al azar dos de ellas con reposición (se extrae la primera, se anota el resultado y nuevamente vuelve al mazo para extraer la segunda), ¿la probabilidad de obtener una carta negra y una figura roja es?
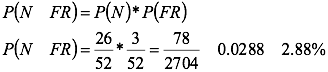
Observe que el número de posibilidades de este suceso “2704”, es similar al del lanzamiento de una moneda, que se puede generalizar así:
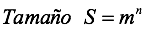
m: El número de opciones
n: Número de ensayos
Para la moneda, si se lanzan tres monedas
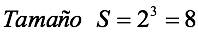
Al extraer dos cartas con reposición
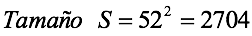
Si se tiene un mazo de 52 cartas y se extraen al azar tres de ellas con reposición (se extrae la primera, se anota el resultado y nuevamente vuelve al mazo para extraer la segunda), ¿la probabilidad de obtener dos figuras y un as es?
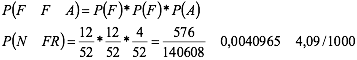
Los sucesos se consideran dependientes si la probabilidad en un segundo suceso se ve afectada por el primero y en el tercero por lo que haya sucedido en el primero y el segundo. Es de anotar que en este tipo de experimentos, el muestreo se realiza sin reposición. El axioma es:
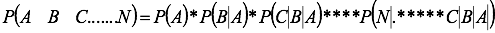
Que se lee: El primer suceso será el número de éxitos sobre el espacio muestral. Para el segundo suceso será la probabilidad del segundo, dado que ya se evaluó la probabilidad del primero y así sucesivamente.
Se realizarán los mismos ejemplos de los sucesos independientes pero con reposición.
Si se tiene un mazo de 52 cartas y se extraen al azar dos de ellas sin reposición, ¿la probabilidad de obtener una carta negra y una figura roja es?
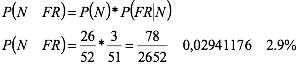
Que fue un poco mayor que si el experimento fuera con reposición, aunque no se puede afirmar que en sucesos dependientes necesariamente la probabilidad es mayor.
Si se tiene un mazo de 52 cartas y se extraen al azar tres de ellas sin reposición, ¿la probabilidad de obtener dos figuras y un as es?
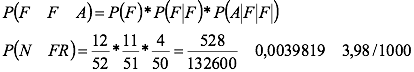
Que fue un poco menor que si el experimento fuera con reposición, lo que comprueba que no se puede afirmar que en experimentos con reposición la probabilidad sea mayor o menor; es necesario evaluarla en cada caso.
Probabilidad condicionalA la probabilidad de que un evento B ocurra cuando se sabe que ya ocurrió un evento A se le llama probabilidad condicional y se denota por:
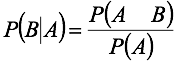
Suponga que se realizó una encuesta donde se les pregunto a hombres y mujeres sobre su situación de empleo, obteniéndose:
| Empelado | Desempleado | Total | |
| Hombre | 490 | 60 | 550 |
| Mujer | 160 | 250 | 410 |
| Total | 650 | 310 | 960 |
Una de estas personas se seleccionará al azar para realizar un viaje con todos los gastos pagos.
Si se llama el evento elegir hombre dado que tiene empleo
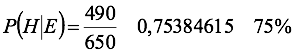
A partir del espacio muestral, se puede deducir la probabilidad que tenga empleo.
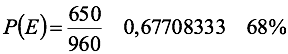
Y de la misma manera, la probabilidad de que en todo el grupo sea elegido un hombre empleado.
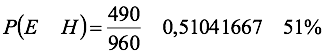
Al aplicar probabilidad condicional, se tiene: