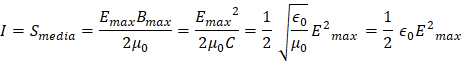El Vector de Poynting
La propagación de la onda es tridimensional, quiere decir que ocupa un volumen en dicha región, éste volumen lo podemos calcular como el área de la superficie por el segmento longitudinal.
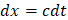
La energía potencial du en ese espacio determinado se calcula por medio del producto del volumen por la densidad de energía u, para ello tenemos:
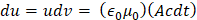
Ahora el flujo de energía que pasa por el área en un tiempo determinado se le conoce el vector de Poynting S. Lo que indica:
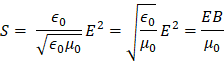
Las unidades para S son:
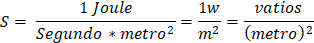
Describiendo vectorialmente ya que los campos magnéticos y eléctricos son vectores, tenemos:
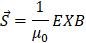
Que s la estructura del vector, introducido por el físico inglés, John Poynting (1854 - 1914). Al calcular la potencia en términos del vector es:
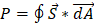
La intensidad de la relación es la medida del vector en cualquier punto en un tiempo dado.
Al variar los campos eléctricos y magnéticos respecto al tiempo, la función S dependerá de estas dos variables, por consiguiente:
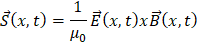
Al sustituir los campos como funciones sinusoidales, tenemos:
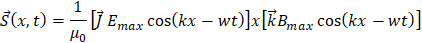
Los vectores anteriores:
 |
y |  |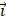
en su producto vectorial nos muestran:
 |
 |
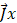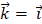Esto corresponde con que la función S nunca es negativa y se propaga en la dirección de x positiva. Al manipular los componentes del vector de Poyinting, tenemos:
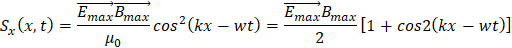
El valor del tiempo medio en la función coseno es cero, ya que por el producto vectorial, coseno no toma valores negativos, lo que conlleva a:
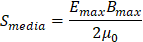
Lo que indica que el valor medio de la intensidad de la onda es: 
del valor máximo. Por lo tanto, el valor de intensidad lo podemos expresar:
