Onda estacionaria

Las funciones de onda asociadas son:

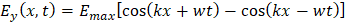
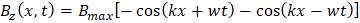
Al revisar los términos de la derecha de las dos ecuaciones notamos que coinciden con las identidades de suma y resta de ángulos para el coseno.

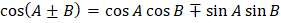
Por lo que los resultados son:

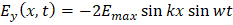
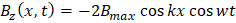
De estas expresiones se concluye que es cero cuando todos los puntos sean perpendiculares al eje x. Estos puntos son válidos para el ángulo kx=0,π,2π…nπ.

Como:

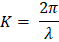
Las posiciones de estos planos son:

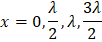
Estos resultados de x son equivalente a los puntos nodales de una onda estacionaria. Para estos nodos los puntos medios oscilan entre sin(⁡kx)= ±1, mientras E_y (x,t) toma el valor máximo posibles de 2E_max lo que indica dos veces en cada ciclo de oscilación conocidos:

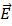
Para el campo magnético se realiza el mismo análisis, este campo magnético total es igual a cero en los planos donde cos(⁡kx)=0, para ello tenemos:

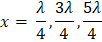
De esta forma se concluye la funcionalidad que tiene sin(⁡wt)=0 para el campo eléctrico y cos⁡(wt)=0 para el campo magnético, ya que indica que mientras uno aumenta el otro disminuye manteniendo como característica particular que están en fase.

En una cavidad la onda estacionaria se comporta igual que una onda mecánica, en este contexto donde E_y (x,t)=0 la longitud de la cavidad L debe ser un múltiplo entero de:

Las longitudes de onda que satisfacen esta condición es:

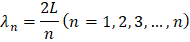
Y sus frecuencias correspondientes son:

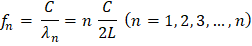
De esta manera, se pueden medir las posiciones nodales y se puede calcular la velocidad de onda. Hertz fue el primero en utilizar esta técnica en la década de los 1880, en sus investigaciones pioneras sobre las ondas electromagnéticas.