La velocidad de una onda electromagnética

Al igualar la fuerza producida por el campo eléctrico F=Eq y el campo magnético F=q(VxB)=qVB tenemos:

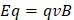
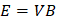
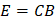
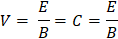
Con C= 3x10⁸m/s (la velocidad de la luz) y la velocidad de propagación de una onda electromagnética en el vacío, otra forma de verificar el valor de la velocidad de una onda electromagnética es utilizando la ley de Gauss para el campo eléctrico de una onda que se desplaza por una distancia x.

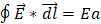
Ahora aplicando la ley de Gauss para campo magnético se tiene que esa onda ha recorrido una distancia en un intervalo de tiempo infinitesimal vdt hacia la derecha. Como este campo es perpendicular al campo eléctrico, la onda ha recorrido un área de tamaño (xvdt), por lo que el flujo aumenta en un factor B(xvdt) y aplicando este factor al flujo magnético tenemos:

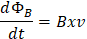
Al tener la ecuación de Faraday y sustituir los dos resultados anteriores se concluye:

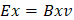
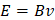
Si es una onda electromagnética su velocidad de propagación es v=C= 3x10⁸m/s donde C es la velocidad de la luz.

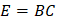
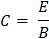
Realizando un cálculo similar pero aplicado la ley de Ampere en el vació, cuando la corriente de conducción es cero tenemos:

El elemento dl debe ser paralelo a la distancia x para que exista por lo que la integral se reduce a:

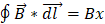
Al considerar que el campo eléctrico y el campo magnético son perpendiculares, el flujo eléctrico en un tiempo infinitesimal recorrerá un área xvdt respecto a la velocidad de propagación de la onda. Al sustituir en la ecuación de flujo tenemos:

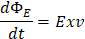
Al sustituir los dos resultados anteriores en la expresión de Ampere tenemos:

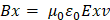
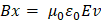
Si empleamos v=c como la velocidad de propagación de la onda en el vacío tenemos:

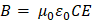
La ley de Faraday y la ley de Ampere se satisfacen si:

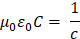o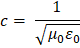

Y al sustituir los valores numéricos de μ₀ y ε₀.

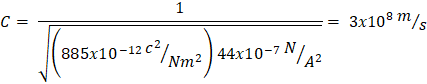
Que es la velocidad de la luz.