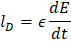Campos eléctricos inducidos

Este campo se puede calcular como:

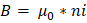
Y sustituyendo esta última expresión en el flujo magnético Φ_B de la espira es:

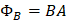
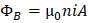
Considerando que la corriente eléctrica y el flujo magnético cambian con el tiempo, la ley de Faraday para la fem inducida en la espira es:

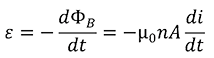
Y utilizando la ley de Ohm, la corriente total se calcula por medio de la resistencia total R.

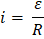
Las cargas se mueven a través de la espira gracias al campo generado por el flujo magnético cambiante. Esta expresión se puede representar:

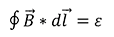
Igualando la fem indicada ε por la ley de Faraday:

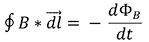
Ahora bien, teniendo en cuenta que la ley de Ampere es:

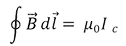
Para un circuito con un capacitor presente la carga Q se incrementa para aumentar el campo eléctrico: 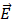entre sus placas, esta corriente se denota como corriente de conducción l_c.

En este capacitor su campo eléctrico 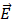y el flujo eléctricos Φ_E aumenta donde su carga instantánea es q=cv donde c es capacitancia y v si diferencia de potencial. Esta capacitancia se calcula como:

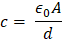
Donde A es el área de cada placa, ϵ₀ la permitividad y d, la distancia entre placas; la diferencia de potencial se calcula como v=Ed donde 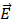es campo eléctrico.

Si q=cv y al sustituir:

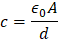
y 𝑣=𝐸𝑑 obtenemos:

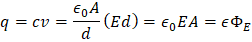
Donde el termino EA=Φ_E que es el flujo eléctrico a través de la superficie. Si:

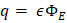
Y al presumir que existe una corriente de desplazamiento ⊥₀ entre las placas del condensador, podemos derivar la expresión anterior respecto al tiempo:

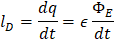
Modificando la ley de Ampere al sumar la corriente de desplazamiento l_D con la de conducción l_c tenemos:

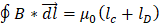
Para una superficie plana l_D=0 y para una superficie curva l_c=0.

Esta variación de la corriente de desplazamiento l_D fue incluida por el físico James Clerk Maxwell (1831 – 1879) en 1865. Por lo tanto, la densidad de corriente de desplazamiento:

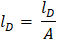
Y tomando el flujo Φ_ϵ=EA podemos encontrar la relación.