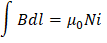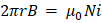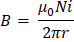Ley de Ampere

Al dividir por segmentos infinitesimales la trayectoria dl para la cual se le asigna la magnitud del campo magnético 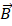y sumando sobre toda la superficie, encontramos la integral de camino:

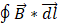
Esta expresión es de carácter escalar.

Para un conductor largo y recto que transporta corriente i el campo magnético tiene una magnitud de:

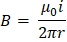
Y al tomar el perímetro de la circunferencia 2πr la integral toma la forma de:

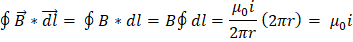
Finalmente la ley de Ampere se puede resumir:

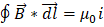
Para calcular el campo en el interior de un conductor largo cilíndrico tenemos como r la distancia del centro hasta los puntos situados dentro del radio R del cilindro. Esto quiere decir que r<R para la parte interna y r>R para la parte externa.

Para la parte interna tenemos:

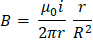
Y para la parte externa tenemos:

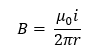
Para un solenoide con número de espiras n en el tramo L, es nL y el campo se calcula:

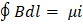
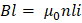
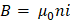
Y para un toroide donde el número de espiras en el devanado es N, la expresión: