Torques y momentos magnéticos
Fuente: Física (p. 923) por Serway, Raymond A., 1994, México: Mc Graw Hill. Derechos de autor, 1994.
Una espira rectangular en presencia de un campo magnético uniforme y paralelo al plano no ejerce fuerza entre los puntos 1 y 3 ya que es paralelo al campo esto es L X B=0, mientras los puntos 2 y 4 son perpendiculares al campo y calculando la magnitud de estas fuerzas tenemos: F=ilB, al sustituir a = L se tiene:
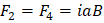
La fuerza generada por 2 sale de la pagina al aplicar la regla de la mano derecha, mientras la fuerza 4 entra a la hoja. Estas dos fuerzas (2,4) producen un torque máximo de:
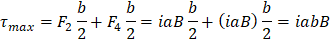
Donde el momento generado está en la posición O calculando por b/2 para cada fuerza. Si el área encerrada por las espira es:
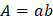
Podemos expresar el torque máximo como:

Si el campo magnético uniforme hace un ángulo θ<90° con la perpendicular la expresión es: τmax=iAB sin∅
El producto iA se conoce como momento dipolar magnético o momento magnético y se representa:
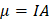
De esta forma el par de torsión en términos del momento magnético es:
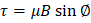
Tanto:
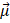 |
como | 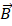 |
Son perpendiculares al plano de rotación, la expresión toma un sentido vectorial, tenemos que:
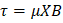
La energía potencial para un polo magnético está determinada por el trabajo que realiza sobre la espira. Esta energía es mínima cuando μ y B son paralelos y máxima cuando son antiparalelos.
Teniendo en cuenta esta conclusión la energía potencial u será calculada así:

