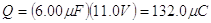Ejemplos de aplicación de las reglas de Kirchhoff
Ejemplo: circuito 2
Determine I1, I2 e I3 en el circuito mostrado en la figura, si tenemos una fuente de voltaje ε1=28V, y otra fuente de voltaje ε2=20V, y sus resistencias R1=8Ω, R2=12Ω y R3=4Ω
Elegimos las direcciones de las corrientes teniendo presente el aumento o la disminución de voltaje en cada elemento presente de la figura. La aplicación de la primera regla de Kirchhoff queda:
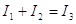 |
(1) |
Hay tres lazos en el circuito, abdca, cdfec y abfea (el lazo exterior). Por lo tanto, necesitamos dos ecuaciones de lazo para determinar las corrientes desconocidas. La tercera ecuación de lazo no brindaría nueva información.
Con la aplicación de la segunda regla de Kirchhoff a los lazos abdca y cdfec y con el recorrido de estos lazos en las direcciones de las manecillas del reloj, obtenemos las expresiones:
| Lazo abdca | 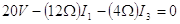 |
(2) |
| Lazo cdfec | 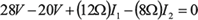 |
(3) |
Adviértase que del lazocdfec se obtiene un signo positivo cuando se recorre el resistor de 12Ω debido a que la dirección de la trayectoria es opuesta a la dirección de I1. Una tercera ecuación de lazo para abdca da 28=4I3+8I2, lo cual es justamente la suma de (2) y (3).
Solución
Las expresiones (1), (2) y (3) representan tres ecuaciones independientes con tres incógnitas. Podemos resolver el problema como sigue: sustituyendo (1) en (2) se obtiene:
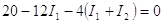 |
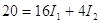 |
(4) |
Al dividir cada término de la ecuación 3 por 2 y ordenar la ecuación, obtenemos:
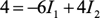 |
(5) |
Al sustraer (5) de (4) se elimina I2 , resulta:
 |
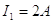 |
Al dividir la ecuación 5 por dos y reemplazar el valor de I1 se obtiene el valor de I2.
Con este valor de I1 en la ecuación 5 se obtiene un valor de I2 :
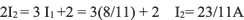 |
Por último, I3=I1+I2=31/11A.
Ejemplo: un circuito de lazos múltiples
En condiciones de estado estable, determine las corrientes desconocidas en el circuito de lazos múltiples mostrado en la figura, si tenemos los siguientes valores de resistencias, para R1=10.00Ω, R2=6.00Ω, R3=10.00Ω y R4=6.00Ω; para las entradas de potencial tenemos una batería de ε1=8.00V y otra de ε2=16.00V y finalmente un condensador de C1=12μF.
Razonamiento
Advierta primero que el capacitor representa un circuito y que, por lo tanto, no hay corriente a lo largo de la trayectoria ghab en condiciones de estado estable. En consecuencia, Igf=I1. Marcando las corrientes de acuerdo lo que indican los lazos marcados con las letras y aplicando la primera regla de Kirchhoff a la unión c, obtenemos:
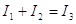 |
(1) |
La segunda regla aplica para los lazos defcd y cfgbc, produce:
| Lazo defcd | 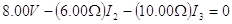 |
(2) |
| Lazo cfgbc | 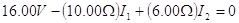 |
(3) |
Solución
En (1) vemos que I1=I3-I2 la cual cuando se sustituye en (3) da:
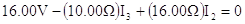 |
(4) |
Restando (4) de (2), eliminamos I3 y encontramos:
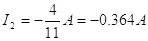
Puesto que I2 es negativa, concluimos que I2 circula de c a f a través del resistor de 6.00Ω. Usando este valor de I2 en (3) y (1), se obtienen los siguientes valores para I1 e I3.
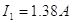 |
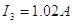 |
En condiciones de estado estable, el capacitor representa un circuito abierto, por lo que, no hay corriente en la rama ghab.
¿Cuál es la carga del capacitor?
Podemos utilizar la segunda regla de Kirchhoff al lazo abgha (o cualquier otro lazo que contenga al capacitor) para determinar la diferencia de potencial V, a través del capacitor:
 |
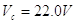 |
Puesto que Q=CVc la carga del capacitor es: