Intensidad y densidad de la corriente

Si denotamos la intensidad de corriente eléctrica como I, al paso de cargas a través de un segmento de área transversal del conductor en función del tiempo tenemos que:

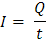
Si tomamos segmentos de área infinitesimal, nuestra definición es:

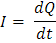
Al utilizar las unidades de medida de carga y tiempo, se detiene la corriente como el Coulomb por un segundo:

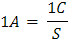
Ahora bien, al considerar que las cargas libres en un conductor son negativas, las velocidades de las cargas tienen la misma dirección que el campo presente; si hay n partículas con carga en movimiento por unidad de volumen y todas las partículas se mueven con la misma velocidad y magnitud Vd.

En un tiempo infinitesimal dt, entonces esta partícula recorre una distancia V_d dt. Al considerar un conductor como un cilindro, el volumen se puede calcular como V= πr² h donde A= πr².

Tomando h como la distancia del cilindro medido en el eje x tenemos x= V^d dt, y sustituyendo:

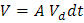
Donde el número de partículas dentro del cilindro es nAV_d dt.

El total de cargas ∆Q es una sección transversal de un conductor, relaciona el número de corrientes en una sección por la corriente de cada carga, en otras palabras.

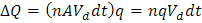
Donde n indica el número de cargas analizadas.

Y la corriente obtiene la siguiente fórmula:

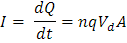
Al considerar la corriente por unidad de área de la sección trasversal del conductor, se le conoce como densidad de corriente J.

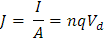
Las unidades son área por metro cuadrado:

Hay que tener en cuenta que el signo de la carga no se incluye en nuestro cálculo, por lo que se sugiere tomar el valor absoluto de |q|.

A diferencia de la corriente eléctrica que es un escalar, la densidad de corriente j es un vector:

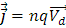
Si q es positiva la velocidad V_d tiene la misma dirección del campo eléctrico, pero si q es negativa la velocidad V_d es opuesta al campo eléctrico. En todo caso la de J es la misma que el campo eléctrico.