Energía potencial eléctrica en un campo eléctrico uniforme

Si el trabajo mecánico realizado por una partícula se calcula mediante el producto de la fuerza aplicada F a una distancia d, entonces se puede calcular de forma escalar como:

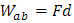
Y si la fuerza presente en un campo eléctrico uniforme, es constante sobre una carga q₀ ,entonces podemos calcular el trabajo realizado de la siguiente forma:

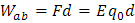
Ahora el cálculo del potencial eléctrico para dos cargas puntuales depende de la diferencia entre sus distancias radiales F_r, así la fuerza generada por cada carga en el campo eléctrico presente se determina por medio de la ley de Coulomb.

De acuerdo con la gráfica, la cual nos muestra dos cargas que se encuentran a diferentes distancias, indica que la diferencia entre r_b y r_a es la distancia que separa las dos cargas y sobre ésta es que actúa la fuerza resultante, para ello tenemos:

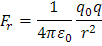
Como la fuerza no es constante durante todo el desplazamiento, se debe realizar la sumatoria infinitesimal de la fuerza, esto es la integral del trabajo. Por ello tenemos:

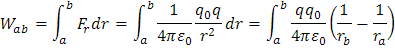
Y para un trabajo realizado por una fuerza que no sigue una distancia radial, tenemos:

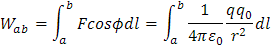
De ésta forma retomando a la expresión que llegamos con fuerzas radiales, podemos calcular la energía potencial de la forma:

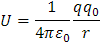
También se puede calcular la energía potencial sustituyendo el término:

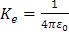
Donde K_e es la constante de Coulomb:

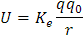
Ejemplo 1

En un acelerador de partículas un electrón de masa 9.1x10^-31 Kg y de carga 1.60x10^-19 C se mueve alrededor de una partícula negativa de 3.20x10^-19 C . Considerando que la partícula negativa está en reposo, cuando se acerca el electrón a una distancia de 10x10^-10 m, adquiere una velocidad de repulsión de 3x10⁶ m/s . ¿Cuál es la rapidez con la que se alejan estas dos partículas si se encuentran a una distancia de 2x10^-10 m?

Solución

Teniendo en cuenta la conservación de la energía para este caso, tenemos:

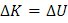
Suponiendo que la partícula negativa y el electrón se encuentran en el instante inicial a una distancia de 10x10^-10 m y la distancia final a 2x10^-10 m, se concluye,

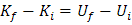
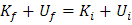
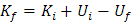
Sustituyendo valores, tenemos:

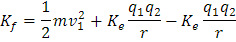
Factorizando:

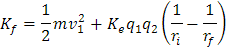
Utilizando los valores del problema, sustituyo y encuentro el valor de energía cinética final K_f :

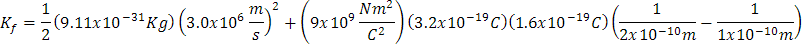
Donde K_f= 6.40x10^-18 J:

Ahora, teniendo en cuenta que el anterior valor es de energía cinética, puedo sustituir:

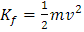
Para encontrar el valor de velocidad de repulsión, para ello tenemos:

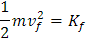
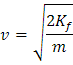
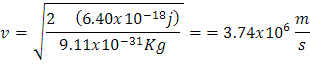
Generalizando una expresión que reúna el cálculo de la energía potencial, con varias cargas puntuales a diferentes distancias y diferentes cargas en relación a q₀ realizamos la suma algebraica del potencial de cada carga, para ello tenemos,

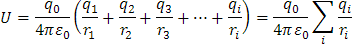
Con esta expresión relacionamos la carga puntual q₀ y un conjunto de cargas q_i.