Dieléctrico dentro de un capacitor
La relación que existe entre la capacitancia de un capacitor con vacío C y un capacitor con dieléctrico presente C0 es:
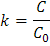
Donde k es la constante dieléctrica del material y es un número adimensional mayor que uno. De esta manera k=1 para el vacío.
De la misma forma en que se puede relacionar las capacitancias, también se pueden relacionar los voltajes obtenidos ya que el valor de la carga es el mismo para los dos casos, por lo tanto tenemos:
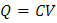
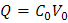
Igualando los dos términos, queda:
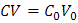
Reordenando términos:
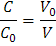
Pero como:
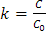 Se sustituye en el término anterior y la expresión toma la forma de:
Se sustituye en el término anterior y la expresión toma la forma de:
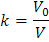
Es decir:
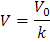
Esto indica que si la carga es una constante, el valor de la diferencia de potencial se reduce en un factor de k cuando hay un dieléctrico presente.
En la siguiente tabla se puede apreciar valores de k para algunos materiales.
Tabla 1. Material.
| Valores de la constante dieléctrica, K, a 20ºC |
|||
| Material | K | Material | K |
| Vacío | 1 | Cloruro de polivinilo | 3.18 |
| Aire (a 1 atm) | 1.00059 | Plexiglás | 3,40 |
| Aire (a 100 atm) | 1.0548 | Vidrio | 5-10 |
| Teflón | 2.1 | Neopreno | 6.70 |
| Polietileno | 2.25 | Germanio | 16 |
| Benceno | 2.28 | Glicerina | 42.5 |
| Mica | 3-6 | Agua | 80.4 |
| Mylar |
3.1 | Titanato de estroncio |
310 |
