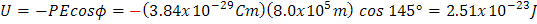Cálculo de pares de torsión en un dipolo eléctrico
Teniendo en cuenta que el momento angular es τ=Fdsenϕ, la fuerza eléctrica es la misma para las dos cargas, a la misma distancia d. El ángulo ϕ se calcula entre el campo eléctrico y el eje del dipolo eléctrico, por lo tanto tenemos:
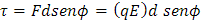
Esta expresión es un producto vectorial.
El producto generado P=qd es llamado el momento dipolar eléctrico y tiene unidades de Cm.
También podemos expresar el momento de torsión de forma vectorial, así:
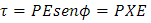
Que se conoce como la energía potencial del dipolo eléctrico sobre un dipolo eléctrico.
Para calcular la energía potencial del dipolo eléctrico se calcula el trabajo realizado dW por un par de torsión en un desplazamiento infinitesimal dϕ, entonces la relación del trabajo y la torsión queda:
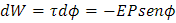
El signo menos indica la disminución de la torsión en la dirección dϕ entonces nuestro cálculo es:
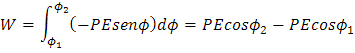
Y teniendo en cuenta que el trabajo es el negativo del cambio de la energía potencial W=U1-U2, nuestro sistema queda:
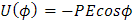
Esta última expresión es un producto escalar y se puede utilizar como:
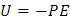
Ejemplo
Un dipolo eléctrico se encuentra en un campo eléctrico de:
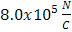
dirigido en forma paralela al plano de las figuras. El dipolo lo integra dos cargas de 3.2x10-19C (una positiva y la otra negativa), y están separadas a una distancia de 0,12x 10 -9m.
Entonces, ¿Cuál es la fuerza neta resultante ejercida por el campo sobre el dipolo, la magnitud y la dirección del momento dipolar eléctrico? Además se debe calcular la magnitud y dirección del par de torsión y la energía potencial del sistema.
Solución:
Para calcular la fuerza neta, se debe tener en cuenta que las cargas son iguales y opuestas, por lo que la fuerza total es cero.
Para calcular el momento dipolar eléctrico P, tenemos:
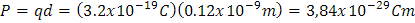
La dirección de P es el de la carga negativa, a 145° en el sentido horario, a partir de la dirección del campo eléctrico.
Para calcular la magnitud del par de torsión es:
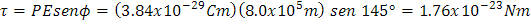
Y para finalizar, la energía potencial la podemos calcular: