Ejercicios
Peralte curva simple
El planteamiento del ejercicio es: En un terreno montañoso para una carretera secundaria de dos carriles; se quiere diseñar una curva circular simple, que cumpla una velocidad (VCH) de 50 Km/h, se utilizará el radio mínimo, asumir que la abscisa del BOP es K0+000, el bombeo de la carretera será del 2%.
Las coordenadas de los alineamientos presentan en la siguiente tabla
Tabla 1. Datos alineamiento
| Norte | Este | |
| BOP | 901.129 | 1124.447 |
| PI | 987.150 | 1218.183 |
| EOP | 897.689 | 1301.581 |
Fuente: elaboración propia.
Calcular el peralte de la curva y presentar el respectivo desarrollo.
Según lo calculado en le capítulo 5 del Manual de Manual de diseño geométrico de carreteras (Invías, 2008), la abscisa del PC es K0 +054.794 y la abscisa del PT es K0 +168.890
Calculo del peralte máximo de la curva
Como se usó el radio mínimo (73m) se utilizara el peralte máximo para carreteras secundarias cuyo valor es 8%.
Si se utiliza un radio mayor; para definir el peralte se utiliza la siguiente tabla.
Tabla 2. Radios, según velocidad especifica y peraltes.
(Para carreteras primarias y secundarias)
| e (%) | VCH = 40 Km/h R(m) | VCH = 50 Km/h R(m) | VCH = 60 Km/h R(m) | VCH = 70 Km/h R(m) | VCH = 80 Km/h R(m) | VCH = 90 Km/h R(m) | VCH = 100 Km/h R(m) | VCH = 100 Km/h R(m) | VCH = 110 Km/h R(m) | VCH = 120 Km/h R(m) |
| 1.5 | 784 | 1090 | 1490 | 1970 | 2440 | 2970 | 3630 | 4180 | 4900 | 5360 |
| 2.2 | 571 | 791 | 1090 | 1450 | 1790 | 2190 | 2680 | 3090 | 3640 | 4000 |
| 2.2 | 512 | 711 | 976 | 1300 | 1620 | 1980 | 2420 | 2790 | 3290 | 3620 |
| 2.4 | 463 | 644 | 885 | 1190 | 1470 | 1800 | 2200 | 2550 | 3010 | 3310 |
| 2.6 | 421 | 587 | 808 | 1080 | 1350 | 1650 | 2020 | 2340 | 2760 | 3050 |
| 2.8 | 385 | 539 | 742 | 992 | 1240 | 1520 | 1860 | 2160 | 2550 | 2830 |
| 3.0 | 354 | 496 | 684 | 916 | 1150 | 1410 | 1730 | 2000 | 2370 | 2630 |
| 3.2 | 326 | 458 | 633 | 849 | 1060 | 1310 | 1610 | 1870 | 2220 | 2460 |
| 3.4 | 3.02 | 425 | 588 | 790 | 988 | 1220 | 1500 | 1740 | 2080 | 2310 |
| 3.6 | 279 | 395 | 548 | 738 | 924 | 1140 | 1410 | 1640 | 1950 | 2180 |
| 3.8 | 259 | 368 | 512 | 690 | 866 | 1070 | 1320 | 1540 | 1840 | 2060 |
| 4.0 | 241 | 344 | 479 | 648 | 813 | 1010 | 1240 | 1450 | 1740 | 1950 |
| 4.2 | 224 | 321 | 449 | 608 | 799 | 948 | 1180 | 1380 | 1650 | 1850 |
| 4.4 | 208 | 301 | 421 | 573 | 722 | 895 | 1110 | 1300 | 1570 | 1760 |
| 4.6 | 192 | 281 | 395 | 540 | 682 | 847 | 1050 | 1240 | 1490 | 1680 |
| 4.8 | 178 | 263 | 371 | 509 | 645 | 803 | 996 | 1180 | 1420 | 1610 |
| 5.0 | 163 | 246 | 349 | 480 | 611 | 762 | 947 | 1120 | 1360 | 1540 |
| 5.2 | 148 | 229 | 328 | 454 | 579 | 724 | 901 | 1070 | 1300 | 1480 |
| 5.4 | 136 | 213 | 307 | 429 | 549 | 689 | 859 | 1020 | 1250 | 1420 |
| 5.6 | 125 | 198 | 288 | 405 | 521 | 656 | 819 | 975 | 1200 | 1360 |
| 5.8 | 115 | 185 | 270 | 382 | 494 | 625 | 781 | 733 | 1150 | 1310 |
| 6.0 | 106 | 172 | 253 | 360 | 469 | 595 | 746 | 894 | 1100 | 1260 |
| 6.2 | 98 | 161 | 238 | 340 | 445 | 567 | 713 | 857 | 1060 | 1220 |
| 6.4 | 91 | 151 | 224 | 322 | 422 | 540 | 681 | 823 | 1020 | 1180 |
| 6.6 | 85 | 141 | 210 | 304 | 400 | 514 | 651 | 789 | 982 | 1140 |
| 6.8 | 79 | 132 | 198 | 287 | 379 | 489 | 620 | 727 | 948 | 1100 |
| 7.0 | 73 | 123 | 185 | 270 | 358 | 464 | 591 | 724 | 914 | 1070 |
| 7.2 | 68 | 115 | 174 | 254 | 338 | 440 | 561 | 691 | 879 | 1040 |
| 7.4 | 62 | 107 | 162 | 237 | 318 | 415 | 531 | 657 | 842 | 998 |
| 7.6 | 57 | 99 | 150 | 221 | 296 | 389 | 499 | 621 | 803 | 962 |
| 7.8 | 52 | 90 | 137 | 202 | 273 | 359 | 462 | 579 | 757 | 919 |
| 8.0 | 41 | 73 | 113 | 168 | 229 | 304 | 394 | 501 | 667 | 832 |
Fuente: Manual de diseño geométrico de carreteras (Invías, 2008).
Calculo de la longitud de transición (L)

Donde:
- L: longitud de transición, en metros.
- a: ancho de la calzada que gira, en metros; a = w*n.
- w: ancho del carril, en metros.
- n: número de carriles que giran.
- bw: factor de ajuste debido al número de carriles que giran.
- (ef – ei): Cambio de peralte, en porcentaje (%).
- Δs: inclinación relativa de la rampa de peraltes.
- El ancho de carril se determina mediante la tabla 2.
- El ancho de carril (w) para el ejemplo es entonces de 3.5 metros
- El número de carriles que giran (n) para carreteras de dos carriles esta determinado igual a 1, según la figura:
Figura 1. Disposición de los carriles que giran respecto a su eje de rotación
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
(Para ampliar la imagen haga clic sobre ella)
| Como | 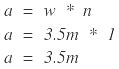 |
El factor de ajuste de acuerdo al número de carriles que giran (bw) es igual a 1; se determina de la tabla:
Tabla 2. Factor de ajuste para el número de carriles girados.
| Número de carriles que giran (n) | Factor de ajuste (bw) | Incremento en los carriles de giro respecto a un carril girado |
| 1.0 | 1.00 | 1.00 |
| 1.5 | 0.83 | 1.25 |
| 2.0 | 0.75 | 1.50 |
| 2.5 | 0.70 | 1.75 |
| 3.0 | 0.67 | 2.00 |
| 3.5 | 0.64 | 2.25 |
Fuente: Manual de diseño geométrico de carreteras (Invías, 2008).
La inclinación relativa de la rampa de peraltes (Δs), depende de la velocidad específica de la curva y se determina con la tabla siguiente:
Tabla 3. Valores máximos y mínimos de la pendiente longitudinal para rampas de peraltes.
| Velocidad específica (VCH) (Km/h) | Pendiente relativa de la rampa de peraltes Δs | |
| Máxima (%) | Mínima (%) | |
| 20 | 1.36 | 0.1 x a |
| 30 | 1.28 | |
| 40 | 0.96 | |
| 50 | 0.77 | |
| 60 | 0.60 | |
| 70 | 0.55 | |
| 80 | 0.50 | |
| 90 | 0.47 | |
| 100 | 0.44 | |
| 110 | 0.41 | |
| 120 | 0.38 | |
| 130 | 0.38 | |
Fuente: Manual de diseño geométrico de carreteras (Invías, 2008).
Entonces;

Cálculo de la longitud de aplanamiento (N)
La longitud de aplanamiento se calcula con la siguiente relación:
Para el desarrollo de un peralte del 8%(valor del peralte calculado para este ejemplo) se necesitan 36.364 metros, cuantos metros se necesitaran para un cambio del 2 % (valor del bombeo para este ejemplo).
Por lo cual la longitud de aplanamiento es de 9.091 metros
Entonces LT= L + N = 45.455 metros
Puntos principales del peralte
El pérlate para una curva circular simple tiene 5 puntos principales:
- A: punto donde empieza el pérlate (los dos bordes tiene le valor del bombeo normal).
- B: punto donde el borde exterior se eleva hasta el 0% y el borde interior sigue con el bombeo normal.
- C: punto donde el borde exterior se eleva hasta un valor del bombeo pero positivo y el borde interior sigue con el valor del bombeo normal.
- D: punto donde empieza la curva (PC) y punto donde termina la curva (PT).
- E: punto donde se presenta el valor máximo del peralte.
Calculo de abscisas del peralte
Para el ejercicio se hará la transición del peralte con la siguiente distribución: el 70% en recta y el 30% en curva, es decir que para el PC y para el PT se tendrá un valor de peralte del 5.6%. las abscisas del peralte en la entrada se calculan desde la abscisa del PC y para la salida se calculan desde la abscisas del PT, tal como se presenta en la tabla:
Tabla 4. Cálculo de abscisas para el desarrollo del peralte
| Cálculo de abscisas | ||
| Entrada | ||
| Punto | Fórmula | Abscisa |
| A | Abscisa del PC -0.7L -N | Ko + 020.248 |
| B | Abscisa de a + N | Ko + 029.339 |
| C | Abscisa de B + N | Ko + 038.430 |
| D (PC) | Abscisa del PC | Ko +157.981 |
| E | Abscisa D + 0.3L | Ko + 065.703 |
| Salida | ||
| Punto | Fórmula | Abscisa |
| E | Abscisa de PT -0.3*L | Ko + 157.981 |
| D (PT) | Abscisa del PT | Ko + 168.890 |
| C | Abscisa PT + 0.7L - N | Ko + 185.254 |
| B | Abscisa C + N | Ko + 194.345 |
| A | Abscisa B + N | Ko + 203.436 |
Fuente: elaboración propia.
Calculo de peralte definitivo para cada abscisa
Para el cálculo del peralte de cada abscisa se hace la siguiente relación:
- En la entrada: En la longitud de transición (L), se desarrolló el máximo peralte (8% para este ejemplo), para una distancia igual a (abscisa de cada punto - las abscisa del punto B), que peralte corresponderá.
- En la salida: En la longitud de transición (L), se desarrolló el máximo peralte (8% para este ejemplo), en una distancia igual a (abscisa del punto B - las abscisa de cada punto), que peralte corresponderá.
Tabla 5. Resultados del cálculo de peralte para cada abscisa.
| Punto | Abscisa | Peralte (%) | |
| Borde derecho | Borde izquierdo | ||
| BOP | 0 | -2.00 | -2.00 |
| 10 | -2.00 | -2.00 | |
| 20 | -2.00 | -2.00 | |
| A | 20.248 | -2.00 | -2.00 |
| B | 29.339 | -2.00 | 0.00 |
| 30 | -2.00 | 0.15 | |
| C | 38.43 | -2.00 | 2.00 |
| 40 | -2.35 | 2.35 | |
| 50 | -4.55 | 4.55 | |
| D(PC) | 54.794 | -5.60 | 5.60 |
| 60 | -6.75 | 6.75 | |
| E | 65.703 | -8.00 | 8.00 |
| 70 | -8.00 | 8.00 | |
| 80 | -8.00 | 8.00 | |
| 90 | -8.00 | 8.00 | |
| 100 | -8.00 | 8.00 | |
| 110 | -8.00 | 8.00 | |
| 120 | -8.00 | 8.00 | |
| 130 | -8.00 | 8.00 | |
| 140 | -8.00 | 8.00 | |
| 150 | -8.00 | 8.00 | |
| E | 157.981 | -8.00 | 8.00 |
| 160 | -7.56 | 7.56 | |
| D (PT) | 168.89 | -5.60 | 5.60 |
| 170 | -5.36 | 5.36 | |
| 180 | -3.16 | 3.16 | |
| C | 185.254 | -2.00 | 2.00 |
| 190 | -2.00 | 0.96 | |
| B | 194.345 | -2.00 | 0.00 |
| 200 | -2.00 | -1.24 | |
| A | 203.436 | -2.00 | -2.00 |
| 210 | -2.00 | -2.00 | |
Fuente: elaboración propia.
A continuación se presenta el diagrama del peralte de la curva circular simple.
Figura 2. Diagrama de peralte.
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
(Para ampliar la imagen haga clic sobre ella)
Ejemplo peralte curva cspiral círculo espiral (ECE)
Dicho ejemplo tiene entre otros los siguientes datos:
- Velocidad específica en la curva: (VCH2) = 60 km/h
- Radio de la curva: (Rc2) = 175.844 m
- Calzada de dos carriles con ancho de carril = 3.65 m
- Abscisa TE = K1 + 239.089
- Abscisa EC = K1 + 309.089
- Abscisa CE = K1 + 393.913
- Abscisa ET = K1 + 463.913
Además se tiene las siguientes especificaciones: carretera secundaria, en un terreno ondulado.
Calculo del peralte máximo de la curva
El valor del peralte se determina según los valores de la tabla 8.6.1 donde se aprecia que para una velocidad de 60 km/h se tienen pos siguientes valores: para un radio de 174 metros corresponde un pérlate de 7.2% y para un radio de 185 metros corresponde un peralte de 7.0%, realizando la correspondiente interpolación se obtiene que para un radio de 175.844 metros el peralte será de 7.17%.
Calculo de la longitud de transición (L)
La longitud de transición para curvas espirales corresponde al mismo valor de la longitud de cada una de las espirales; por lo cual L = Le = 70 metros. Lo que indica que la transición del peralte en la entrada de la curva se realizara desde el TE hasta el EC, la curva circular central tendrá un peralte máximo en toda su longitud y la transición en la salida de la curva se hará desde el Et hasta el CE.
Cálculo de la longitud de aplanamiento (N)
La longitud de aplanamiento se calcula con las siguientes relaciones:
Para el desarrollo de un peralte del 7.17 % se utilizaran 70 metros, para un cambio del 2%, cuantos metros se necesitaran?
p>N = 19.526 metros
Puntos principales del peralte
El pérlate para una curva espiral circulo espiral tiene 4 puntos principales:
- A: punto donde empieza el pérlate (los dos bordes tiene le valor del bombeo normal)
- B: punto donde el borde exterior se eleva hasta el 0% y el borde interior sigue con el bombeo normal, este punto esta ubicado para la espiral de entrada en la abscisa del TE y ara la espiral de salida en la abscisa del ET
- C: punto donde el borde exterior se eleva hasta un valor del bombeo pero positivo y el borde interior sigue con el valor del bombeo normal.
- D: punto donde empieza el peralte máximo, este punto esta ubicado para la espiral de entrada en la abscisa del EC y ara la espiral de salida en la abscisa del CE.
alculo de abscisas del peralte
Las abscisas del peralte en la entrada se calculan desde la abscisa del TE y para la salida se calculan desde las abscisas del ET tal como se presenta en la tabla 6.
Tabla 6. Cálculo de Abscisas del peralte.
| Cálculo de abscisas | ||
| Entrada | ||
| Punto | fórmula | Abscisa |
| A | Abscisa del TE - N | K1 + 219.563 |
| B (TE) | Abscisa del TE | K1 + 239.089 |
| C | Abscisa del TE + N | K1 + 258.615 |
| D (EC) | Abscisa del EC | K1 + 309.089 |
| Salida | ||
| Punto | Fórmula | Abscisa |
| D (CE) | Abscisa del CE | K1 + 393.913 |
| C | Abscisa del ET - N | K1 + 444.387 |
| B (ET) | Abscisa del ET | K1 + 463.913 |
| A | Abscisa del ET + N | K1 + 483.439 |
Fuente: elaboración propia.
Calculo de peralte definitivo para cada abscisa
Para el cálculo del peralte de cada abscisa se hace la siguiente relación:
- En la entrada: En la longitud de la espiral, se desarrolló un peralte de 7.17%, para una distancia igual a (abscisa de cada punto - la abscisa del punto B), que peralte corresponderá?
- En la salida: En la longitud de la espiral, se desarrolló un peralte de 7.17%, en una distancia igual a (abscisa del punto B - la abscisa de cada punto), que peralte corresponderá?
En toda la curva circular central se presente el peralte máximo.
Los resultados de peralte para cada abscisa se presentan en la siguiente tabla:
Tabla 7. Cálculo de peralte para cada abscisa.
| Punto | Abscisa | Peralte (%) | |
| Borde derecho | Borde izquierdo | ||
| A | 1219.59 | -2.00 | -2.00 |
| 1220 | -2.00 | -1.96 | |
| 1230 | -2.00 | -0.93 | |
| B (TE) | 1239.089 | -2.00 | 0.00 |
| 1240 | -2.00 | 0.09 | |
| 1250 | -2.00 | 1.12 | |
| C | 1258.588 | -2.00 | 2.00 |
| 1260 | -2.14 | 2.14 | |
| 1270 | -3.17 | 3.17 | |
| 1280 | -4.20 | 4.20 | |
| 1290 | -5.22 | 5.22 | |
| 1300 | -6.25 | 6.25 | |
| D | 1309.089 | -7.18 | 7.18 |
| 1310 | -7.18 | 7.18 | |
| 1320 | -7.18 | 7.18 | |
| 1330 | -7.18 | 7.18 | |
| 1340 | -7.18 | 7.18 | |
| 1350 | -7.18 | 7.18 | |
| 1360 | -7.18 | 7.18 | |
| 1370 | -7.18 | 7.18 | |
| 1380 | -7.18 | 7.18 | |
| 1390 | -7.18 | 7.18 | |
| D | 1393.913 | -7.18 | 7.18 |
| 1400 | -6.56 | 6.56 | |
| 1410 | -5.53 | 5.53 | |
| 1420 | -4.50 | 4.50 | |
| 1430 | -3.48 | 3.48 | |
| 1440 | -2.45 | 2.45 | |
| C | 1444.414 | -2.00 | 2.00 |
| 1450 | -2.00 | 1.43 | |
| 1460 | -2.00 | 0.40 | |
| B (TE) | 1463.913 | -2.00 | 0.00 |
| 1470 | -2.00 | -0.62 | |
| 1480 | -2.00 | -1.65 | |
| A | 1483.412 | -2.00 | -2.00 |
Fuente: elaboración propia.
A continuación se presenta el diagrama del peralte de la curva espiral círculo espiral:
Figura 3. Diagrama de peralte de la curva ECE.
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
(Para ampliar la imagen haga clic sobre ella)
