Determinación de la curva vertical cóncava
Para determinar la longitud mínima de la curva vertical es necesario verificar los criterios de operación y de seguridad, el primero establece que:
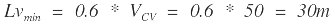
Como el abscisado es de 10 metros la longitud mínima por operación será de 40 metros, de manera tal que a cada lado del PIV se tengan 20 metros de curva.
Por el criterio de seguridad es necesario establecer si la longitud mínima de la curva es menor o mayor que la distancia de visibilidad que se quiere analizar, para lo cual es necesario determinar los dos valores y verificar cual cumple el condicionamiento del caso:
Primero se determina el valor de la diferencia algebraica de pendientes A:
| Caso I. (DV > Lv) | 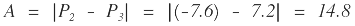 |
| Caso II. (DV < Lv) | 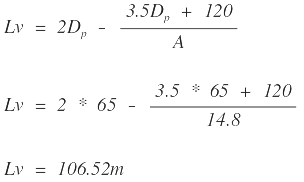 |
Como se observa se cumple el caso II, ya que la distancia de visibilidad analizada es menor que la longitud hallada (65 < 179,94). Por lo tanto la longitud mínima que se puede emplear para la curva cóncava del PIV2 es de 180 metros. La figura 1 y la tabla 1 presentan el diseño de rasante definitivo para las dos curvas:
Figura 1. Rasante con las longitudes mínimas de Lv.
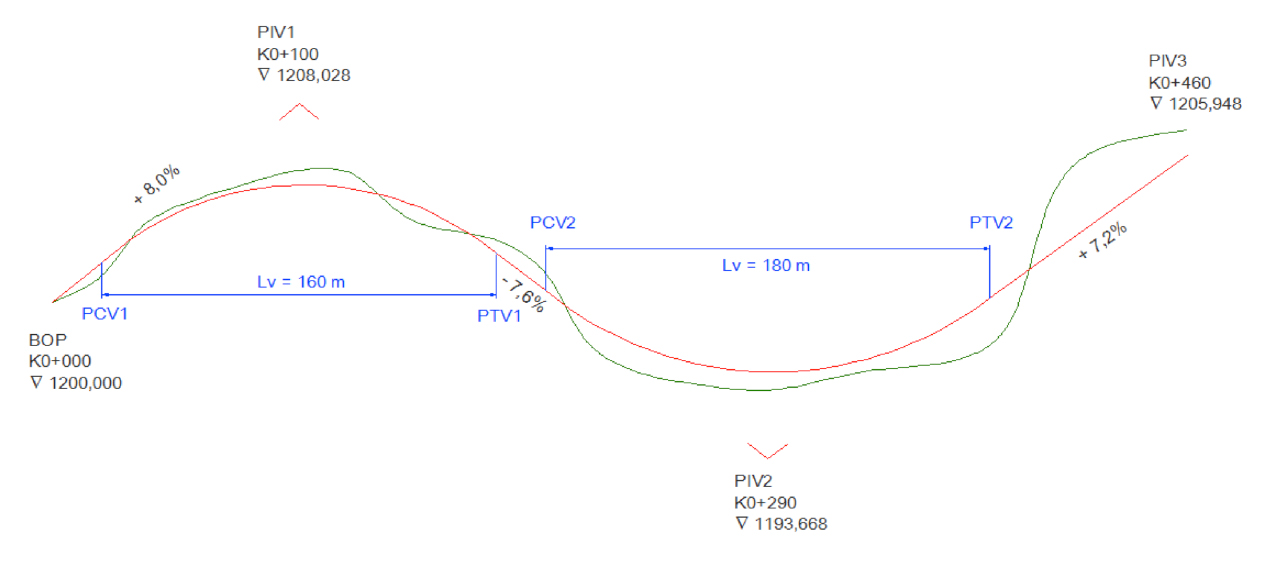
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
(Para ampliar la imagen haga clic sobre ella)
Tabla 1. Cartera de rasante curvas simétricas.
| ABSC | ∇ terreno | ∇ tangente | P | y | ∇ rasante | H. de trabajo | |
| PCV1 | K0+000 | 1200.000 | 1200.000 | 8.0 | 1200.000 | 0.000 | |
| K0+010 | 1200.412 | 1200.803 | 1200.803 | 0.391 | |||
| K0+020 | 1201.061 | 1201.606 | 0.000 | 1201.606 | 0.545 | ||
| K0+030 | 1202.339 | 1202.408 | 0.049 | 1202.360 | 0.021 | ||
| K0+040 | 1203.336 | 1203.211 | 0.195 | 1203.016 | -0.320 | ||
| K0+050 | 1203.849 | 1204.014 | 0.439 | 1203.575 | -0.274 | ||
| K0+060 | 1204.214 | 1204.817 | 0.780 | 1204.037 | -0.177 | ||
| K0+070 | 1204.527 | 1205.620 | 1.219 | 1204.401 | -0.126 | ||
| K0+080 | 1204.824 | 1206.422 | 1.755 | 1204.667 | -0.157 | ||
| K0+090 | 1205.124 | 1207.255 | 2.389 | 1204.836 | -0.288 | ||
| PIV1 | K0+100 | 1205.335 | 1208.028 | 3.120 | 1204.908 | -0.427 | |
| K0+110 | 1205.425 | 1207.272 | -7.6 | 2.389 | 1204.883 | -0.542 | |
| K0+120 | 1205.249 | 1206.516 | 1.755 | 1204.761 | -0.488 | ||
| K0+130 | 1204.565 | 1205.761 | 1.219 | 1204.542 | -0.023 | ||
| K0+140 | 1203.683 | 1205.005 | 0.780 | 1205.225 | 0.542 | ||
| K0+150 | 1203.153 | 1204.249 | 0.439 | 1203.810 | 0.657 | ||
| K0+160 | 1202.911 | 1203.493 | 0.195 | 1203.298 | 0.387 | ||
| K0+170 | 1202.767 | 1202.737 | 0.049 | 1202.689 | -0.078 | ||
| PTV1 | K0+180 | 1202.502 | 1201.982 | 0.000 | 1201.982 | -0.520 | |
| K0+190 | 1202.022 | 1201.226 | 1201.226 | -0.796 | |||
| PCV2 | K0+200 | 1201.155 | 1200.470 | 0.000 | 1200.470 | -0.685 | |
| K0+210 | 1199.428 | 1199.714 | 0.041 | 1199.755 | 0.327 | ||
| K0+220 | 1198.075 | 1198.959 | 0.164 | 1199.123 | 1.048 | ||
| K0+230 | 1197.437 | 1198.203 | 0.370 | 1198.573 | 1.136 | ||
| K0+240 | 1197.092 | 1197.447 | 0.658 | 1198.105 | 1.013 | ||
| K0+250 | 1196.856 | 1196.691 | 1.028 | 1197.719 | 0.863 | ||
| K0+260 | 1196.377 | 1195.935 | 1.480 | 1197.415 | 1.038 | ||
| K0+270 | 1196.683 | 1195.180 | 2.014 | 1197.194 | 0.511 | ||
| K0+280 | 1196.436 | 1194.424 | 2.631 | 1197.055 | 0.619 | ||
| PIV2 | K0+290 | 1196.435 | 1193.668 | 3.330 | 1196.998 | 0.563 | |
| K0+300 | 1196.559 | 1194.390 | 7.2 | 2.631 | 1197.021 | 0.462 | |
| K0+310 | 1196.771 | 1195.113 | 2.014 | 1197.127 | 0.356 | ||
| K0+320 | 1197.026 | 1195.835 | 1.480 | 1197.315 | 0.289 | ||
| K0+330 | 1197.262 | 1196.557 | 1.028 | 1197.585 | 0.323 | ||
| K0+340 | 1197.429 | 1197.280 | 0.658 | 1197.938 | 0.509 | ||
| K0+350 | 1197.508 | 1198.002 | 0.370 | 1198.372 | 0.864 | ||
| K0+360 | 1197.569 | 1198.724 | 0.164 | 1198.889 | 1.320 | ||
| K0+370 | 1197.719 | 1199.447 | 0.041 | 1199.488 | 1.769 | ||
| PTV2 | K0+380 | 1198.180 | 1200.169 | 0.000 | 1200.169 | 1.989 | |
| K0+390 | 1199.604 | 1200.892 | 1200.892 | 1.287 | |||
| K0+400 | 1202.878 | 1201.614 | 1201.614 | -1.264 | |||
| K0+410 | 1205.115 | 1202.336 | 1202.336 | -2.779 | |||
| K0+420 | 1205.997 | 1203.059 | 1203.059 | -2.938 | |||
| K0+430 | 1206.408 | 1203.781 | 1203.781 | -2.627 | |||
| K0+440 | 1206.667 | 1204.503 | 1204.503 | -2.164 | |||
| K0+450 | 1206.832 | 1205.226 | 1205.226 | -1.606 | |||
| PIV3 | K0+460 | 1206.961 | 1205.948 | 1205.948 | -1.013 | ||
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
