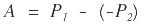Cálculo de la parábola en el punto A
Para la parábola en el punto A se tiene:
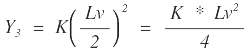
Remplazando P1 y Y3 en la ecuación de la tangente y evaluando el punto B (0, Y4) se tiene:
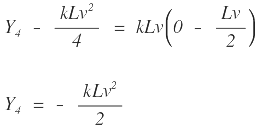
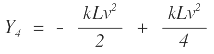
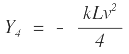
Ténganse en cuenta que los valores absolutos de Y3 y Y4 son iguales, por lo tanto CB = CD, importante propiedad de la parábola, la cual establece que la externa es igual a la flecha.
La ecuación de la tangente también puede darse considerando su pendiente P1 y el punto Q:
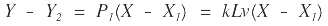
Evaluando en el punto A
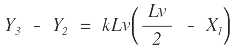 |
Remplazando Y3 y despejando Y2, se obtiene: |
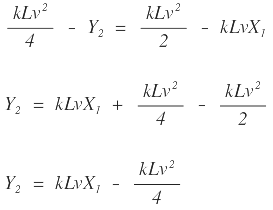
Para la parábola en l punto P se tiene que Y1 = k X12, realizando la diferencia entre Y1 y Y2 se obtiene:
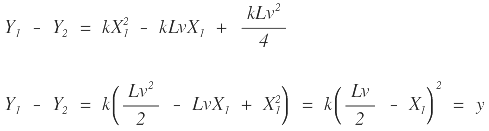
En lo anterior se observa que:
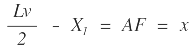 |
y |
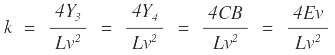 |
, por lo tanto: |
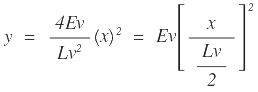
Donde “y” se conoce como la corrección por pendiente en función de la externa y con origen en el punto A o PCV
Por otra parte, teniendo en cuenta la simetría de la figura se tiene que pero como se obtiene y por tanto
| Ahora | 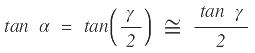 |
remplazando los valores de las tangentes | 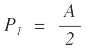 |
| Retomando | 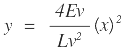 |
y organizando factores: |
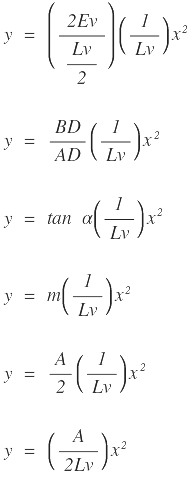
x = Distancia horizontal a cualquier punto de la curva desde el PCV (en metros)
y = Ordenada vertical en cualquier punto (p) y, se calcula mediante la expresión.
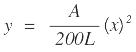
En la cual la diferencia de pendientes está expresada en porcentaje.
Esta ordenada se le resta a las cotas de las tangentes en las curvas verticales convexas y se suma, en las cóncavas.
| Para | 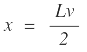 |
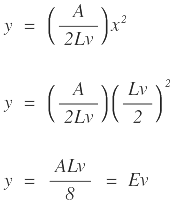
Ev = Externa: ordenada vertical desde el PIV a la curva.
Expresando la diferencia de pendientes en porcentaje:
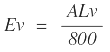
Por otra parte, considerando el punto p’ ubicado en la segunda mitad de la curva, para localizarlo desde el punto E o PTV, interesa conocer la distancia x’ y la altura y’.

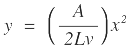 |
, referido al punto A. | 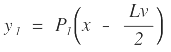 |
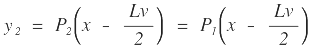 |
Por lo tanto:
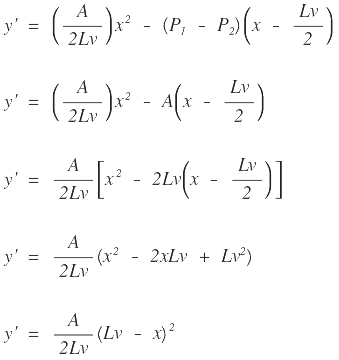
pero como Lv - x = x’ entonces:
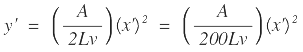
x’ es la distancia medida desde el punto E o PTV al punto p’
Lo anterior determina que la primera mitad de la curva se calcula desde el PCV y la segunda desde el PTV.
En la generalidad del trazado las pendientes de entrada y salida no son iguales (α ≠ β), tal como se puede observar en la figura 1, y por tanto se tendrá:
Figura 1. Diferencia algebraica de pendientes
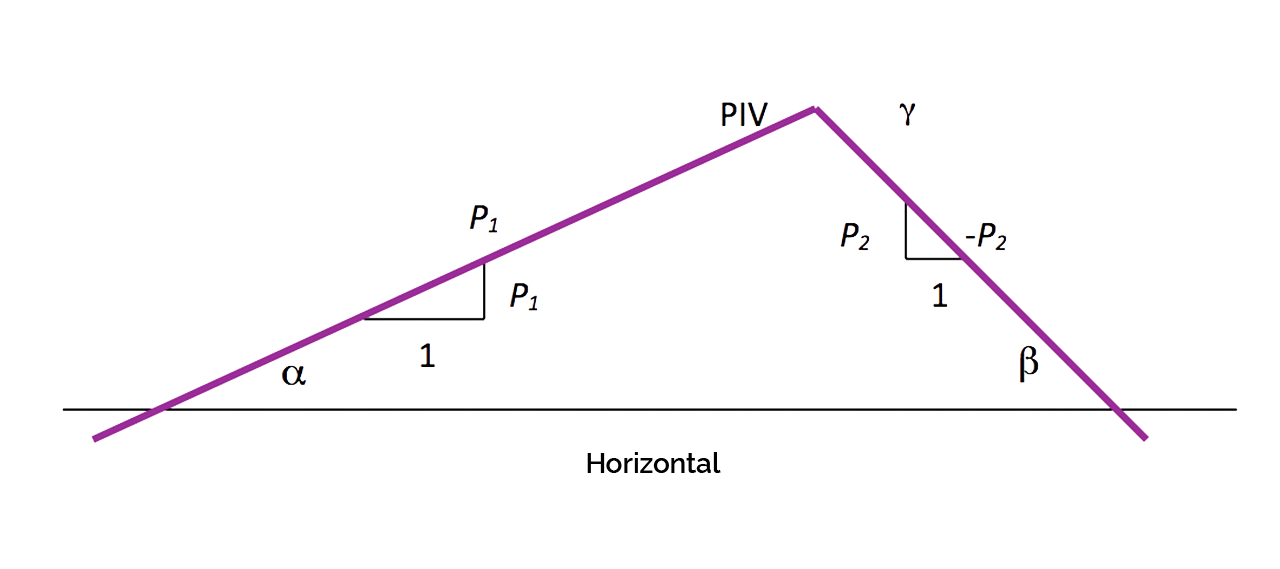
Fuente: (Vargas Vargas, Gonzalez Vergara, & Rincon Villalba, 2013)
(Para ampliar la imagen haga clic sobre ella)
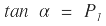 |
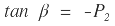 |
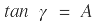 |
sabiendo que: | 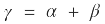 |
tenemos que: |
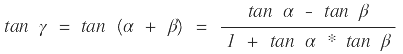
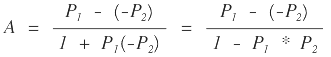
Para carreteras las pendientes máximas son del orden del 14% (0.14), razón por la cual el producto máximo será: P1 * P2 = 0.14 * 0.14 =0.0196, es despreciable frente a la unidad, por tanto