Ejemplo de una curva espiral círculo espiral ECE
Planteamiento
Se desea diseñar un empalme espiralizado en el PI2 del alineamiento de una vía, del cual se conocen los siguientes datos:
| Coordenadas del PI2: (N,E) | 1098789.000, 1096930.570 |
| Distancia del PI1 al PI2: (d12) | 532.623 m |
| Azimut del PI1 al PI2: (Azimut de entrada Az12) | 148º 40’ 42’’ |
| Azimut del PI2 al PI3: (Azimut de entrada Az23) | 199º 07’ 30’’ |
| Velocidad específica en la curva: (VCH2) | 60 km/h |
| Radio de la curva: (Rc2) | 175.844 m |
| Calzada de dos carriles con ancho: (a) | 3.65 m |
| Abscisa del ET1 | K0+902064 |
| Tangente de la curva 1: (Te1) | 77.264 m |
Determinación de los valores límite de diseño
Se deben establecer los valores de longitud de espiral mínima y máxima que pueden ser empleados:
Valores mínimos: criterio I de la ecuación tenemos
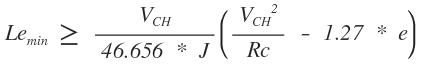
De la tabla del manual se tiene para una velocidad de 60 km/h
| e (%) | Rc (m) |
| 7.0 | 185 |
| 7.2 | 174 |
Realizando la interpolación para Rc = 175.844 m se obtiene un peralte de 7.17%
De la Tabla 15 para una velocidad de 60 km/h se obtiene un J = 0.7 m/s3
Remplazando en la ecuación obtenemos:
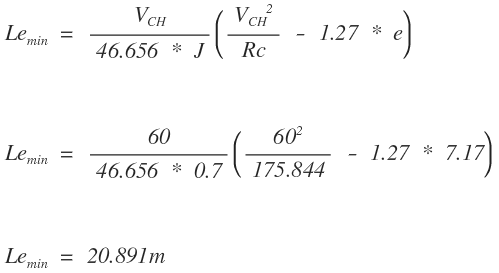
Criterio II. Se tiene la ecuación
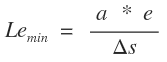
De la tabla del manual se tiene para una velocidad de 60 km/h que Δs máximo es 0.60%. Remplazando valores en la ecuación obtenemos:
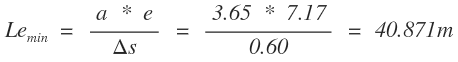
Criterio III.1 Se tiene la ecuación
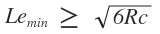
Remplazando valores en la ecuación obtenemos:
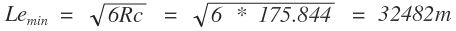
Criterio III.2 Se tiene la ecuación
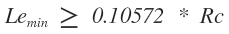
Remplazando valores en la ecuación obtenemos:
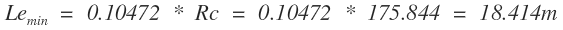
Valor máximo: de la ecuación
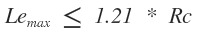
Remplazando valores en la ecuación obtenemos:
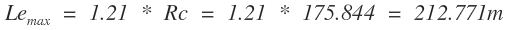
Por lo tanto los valores límite de diseño son:
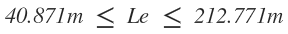
Verificación del empalme ECE
Se debe establecer el valor del ángulo de giro de la espiral (θe) y el valor del segmento circular de la curva el cual debe ser mayor a la distancia recorrida en 2 segundos a la velocidad específica de la curva, de cumplirse esto el empalme es ECE:
De la ecuación hallamos el valor de θe partiendo de un valor de Le = 70 m, escogido arbitrariamente entre el rango establecido en el numeral anterior.
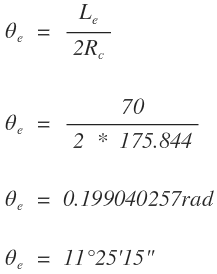
En la figura 1 se observa que el ángulo de deflexión del empalme es igual a la suma de los ángulos de giro de las espirales y el ángulo de giro del segmento circular:
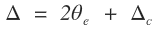
pero también
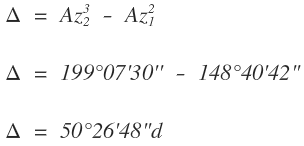
Por lo tanto
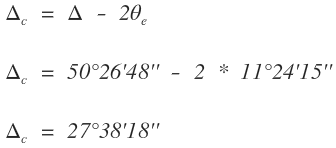
Se determina la longitud del segmento circular (Lc) y se verifica con su valor mínimo:
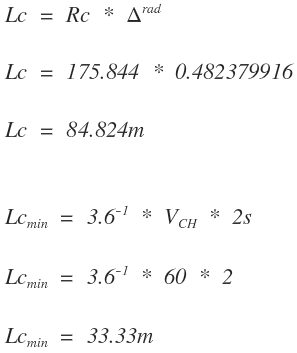
como Lc > Lcmin el empalme es ECE.
Determinación de los elementos del empalme ECE
El parámetro de la espiral (A) se halla de la ecuación
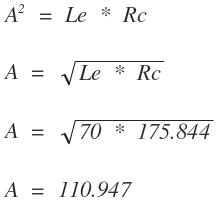
Las ecuaciones paramétricas (X y Y) se halla de las ecuaciones
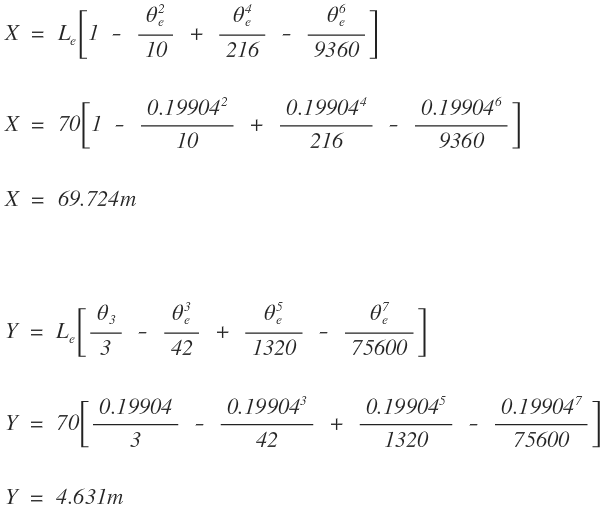
El disloque (ΔR) se halla de la ecuación
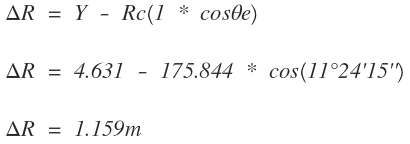
La abscisa media (XM) se halla de la ecuación
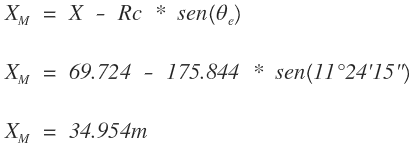
La tangente larga (Tl) se halla de la ecuación
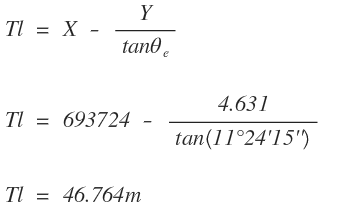
La tangente corta (Tc) se halla de la ecuación
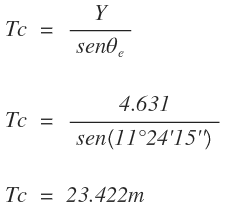
La tangente del empalme (Te) se halla de la ecuación
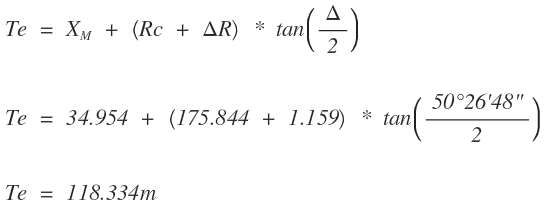
La externa o bisectriz del empalme (Ee) se halla con la ecuación
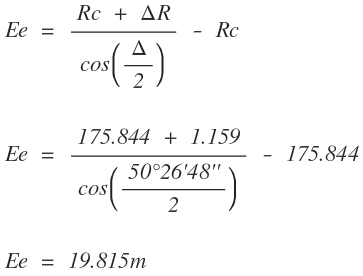
La deflexión última de la espiral (ϕe) se halla con la ecuación
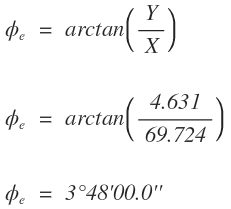
La cuerda larga de la espiral (CLe) se halla con la ecuación
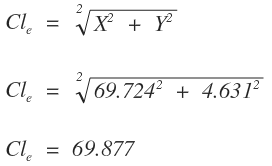
Cálculo de la cartera de tránsito: deflexiones y coordenadas de todos los puntos del empalme ECE.
Para realizar la cartera de tránsito y establecerlas coordenadas de todos los puntos del empalme para su posterior localización es necesario en primera instancia determinar las abscisas de los puntos especiales (TE, EC, CE, ET), estableciendo cuales son las abscisas completas del proyecto con conforman las ramas de espiral y el segmento circular.
Para las abscisas o puntos de una espiral se determina la longitud del punto al origen de la espiral (Lp) y con ella se calcula el ángulo de giro del punto (θp) con el cual se halla tanto la deflexión del punto (ϕp), como su cuerda larga (CLp). Para los puntos del segmento circular se determinan las deflexiones (δp) y la cuerda larga (CLp)
Tanto en las ramas de espiral como en el segmento circular se calculan las coordenadas de cada punto (Np, Ep) utilizando las deflexión y la cuerda larga del punto. Para ello de debe determinar previamente las coordenadas del TE y del ET; el cierre de coordenadas se realiza en el CE.
Determinación del abscisado del empalme:

La tabla 16 presenta la cartera de tránsito para el empalme, de acuerdo con el abscisado antes definido.
Determinación de las coordenadas del TE2 y del ET2
Las coordenadas del TE2 y del ET2 se determinan con base en las coordenadas del PI2, la Te del empalme y los azimut de entrada y salida:

Determinación de la deflexión y coordenadas de los puntos del empalme.
La determinación de la deflexión y cada punto de las ramas de espiral así como del segmento circular obedecen a un cálculo secuencial reiterativo, como ejemplo se ilustra un punto de cada uno de los segmentos del empalme. La totalidad de los cálculos se presentas en la Tabla 16.
Espiral de entrada – Abscisa K1+280
La longitud Lp de la abscisa es la distancia entre el punto y el origen de la espiral
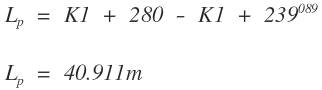
Ángulo de giro de la abscisa
Ángulo de giro de la abscisa
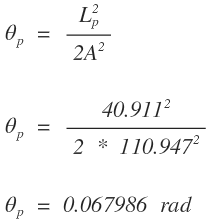
Ecuaciones paramétricas o coordenadas cartesianas de la abscisa
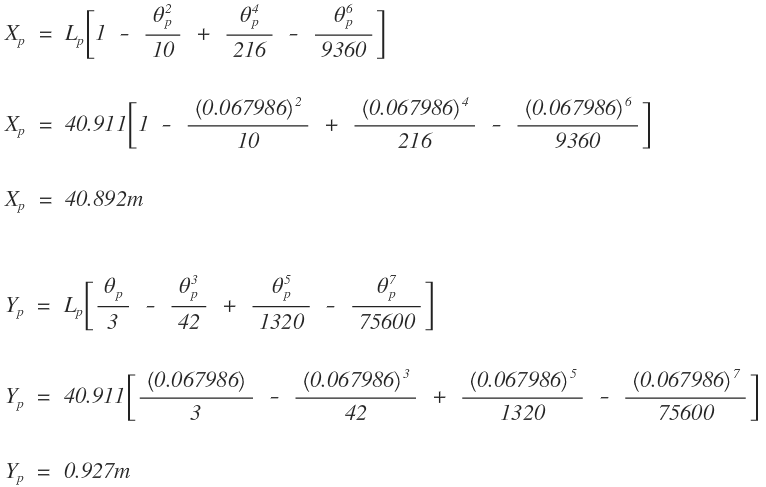
Cuerda larga de la abscisa
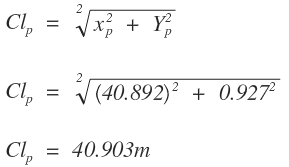
Deflexión de la abscisa
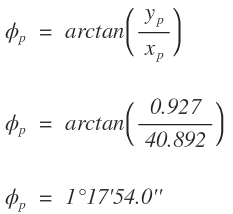
Coordenadas planas de la abscisa

Con este procedimiento se determinan las deflexiones y coordenadas de todos los puntos de la espiral de entrada incluido el EC
Segmento circular – Abscisa K1+340
La deflexión y la cuerda larga se determinan de manera similar a una curva circular simple, los coordenadas se basa en el EC.
Determinación del grado de curvatura
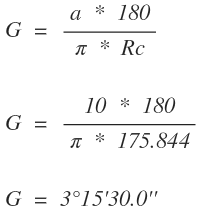
Deflexión de la abscisa
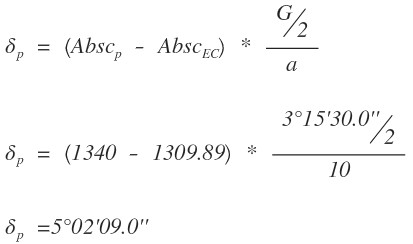
Cuerda larga de la abscisa
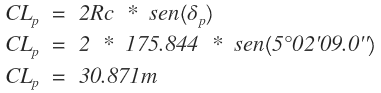
Coordenadas planas de la abscisa
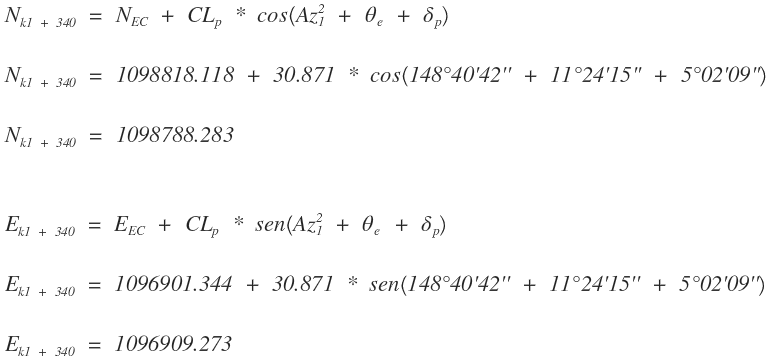
Con este procedimiento se determinan las deflexiones y coordenadas de todos los puntos del segmento circular incluido el CE
Espiral de salida – Abscisa K1+430
La longitud Lp de la abscisa es la distancia entre el punto y el origen de la espiral
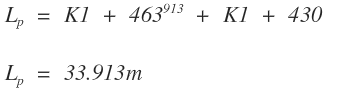
Ángulo de giro de la abscisa
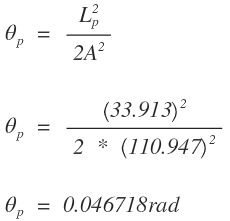
Ecuaciones paramétricas o coordenadas cartesianas de la abscisa

Cuerda larga de la abscisa
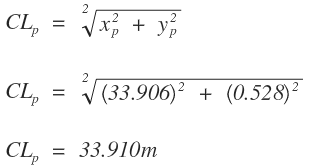
Deflexión de la abscisa
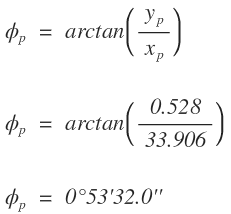
Coordenadas planas de la abscisa

Con este procedimiento se determinan las deflexiones y coordenadas de todos los puntos de la espiral de salida, incluido el CE. Se verifica que las coordenadas de EC sean iguales a las calculadas por el segmento circular.
Tabla 16: cartera de transito del empalme ECE – curva del PI
| Abscisa | Lp | Deflexiones | θp = | CL = | Coor. cartesianas | Coor. planes | ||
| x | y | Norte | Este | |||||
| ET K1 + 463.913 | 0.000 | 0°0'0'' | 0.000000 | 0.000 | 0.000 | 0.000 | 1 098 667.197 | 1 096 891.800 |
| K1 + 460.000 | 3.913 | 0°0'43.0'' | 0.000622 | 3.913 | 3.913 | 0.001 | 1 098 670.895 | 1 096 893.082 |
| K1 + 450.000 | 13.913 | 0°9'1.0'' | 0.007863 | 13.913 | 13.913 | 0.036 | 1 098 680.355 | 1 096 896.324 |
| K1 + 440.000 | 23.913 | 0°26'37.0'' | 0.023229 | 23.913 | 23.912 | 0.185 | 1 098 689.850 | 1 096 899.460 |
| K1 + 430.000 | 33.913 | 0°53'32.0'' | 0.046718 | 33.910 | 33.906 | 0.528 | 1 098 699.405 | 1 096 902.410 |
| K1 + 420.000 | 43.913 | 1°29'45.0'' | 0.078331 | 43.901 | 43.886 | 1.146 | 1 098 709.037 | 1 096 905.096 |
| K1 + 410.000 | 53.913 | 2°15'17.0'' | 0.118068 | 53.880 | 53.838 | 2.120 | 1 098 718.758 | 1 096 907.437 |
| K1 + 400.000 | 63.913 | 3°10'6.0'' | 0.165939 | 63.835 | 63.738 | 3.528 | 1 098 728.573 | 1 096 909.349 |
| CE K1 + 393.913 | 70.000 | 3°48'0.0'' | 0.199040 | 69.877 | 69.724 | 4.631 | 1 098 734.590 | 1 096 910.268 |
| CE K1 + 393.913 | 70.000 | 13°49'9.0'' | 0.199040 | 84.004 | 69.724 | 4.631 | 1 098 734.590 | 1 096 910.268 |
| k1 + 390.000 | 0.000 | 13°10'54.0'' | 0.000000 | 80.199 | 0.000 | 0.000 | 1 098 738.473 | 1 096 910.751 |
| K1 + 380.000 | 0.000 | 11°33'9.0'' | 0.000000 | 70.431 | 0.000 | 0.000 | 1 098 748.436 | 1 096 911.591 |
| K1 + 370.000 | 0.000 | 9°55'24.0'' | 0.000000 | 60.607 | 0.000 | 0.000 | 1 098 758.431 | 1 096 911.862 |
| K1 + 360.000 | 0.000 | 8°17'39.0'' | 0.000000 | 50.733 | 0.000 | 0.000 | 1 098 768.425 | 1 096 911.566 |
| K1 + 350.000 | 0.000 | 6°39'54.0'' | 0.000000 | 40.818 | 0.000 | 0.000 | 1 098 778.387 | 1 096.910.702 |
| K1 + 340.000 | 0.000 | 5°2'9.0'' | 0.000000 | 30.871 | 0.000 | 0.000 | 1 098 788.283 | 1 096 909.273 |
| K1 + 330.000 | 0.000 | 3°24'24.0'' | 0.000000 | 20.898 | 0.000 | 0.000 | 1 098 798.081 | 1 096 907.284 |
| K1 + 320.000 | 0.000 | 1°46'39.0'' | 0.000000 | 10.909 | 0.000 | 0.000 | 1 098 807.751 | 1 096 904.741 |
| K1 + 310.000 | 0.000 | 0°8'54.0'' | 0.000000 | 0.911 | 0.000 | 0.000 | 1 098 817.261 | 1 096 901.652 |
| EC K1 + 309.089 | 70.000 | 0°0'0.0'' | 0.199040 | 69.877 | 69.724 | 4.631 | 1 098 818.118 | 1 096 901.344 |
| EC K1 + 309.089 | 70.000 | 3°48'0.0'' | 0.199040 | 69.877 | 69.724 | 4.631 | 1 098 818.118 | 1 096 901.344 |
| K1 + 300.000 | 60.911 | 2°52'40.0'' | 0.150706 | 60.850 | 60.773 | 3.055 | 1 098 826.584 | 1 096 896.038 |
| K1 + 290.000 | 50.911 | 2°0'38.0'' | 0.105284 | 50.886 | 50.855 | 1.758 | 1 098 835.716 | 1 096 893.967 |
| K1 + 280.000 | 40.911 | 1°17'54.0'' | 0.067986 | 40.903 | 40.892 | 0.927 | 1 098 844.673 | 1 096 889.521 |
| K1 + 270.000 | 30.911 | 0°44'28.0'' | 0.038812 | 30.909 | 30.906 | 0.400 | 1 098 853.478 | 1 096 884.780 |
| K1 + 260.000 | 20.911 | 0°20'21.0'' | 0.017762 | 20.911 | 20.910 | 0.124 | 1 098 862.160 | 1 096 879.820 |
| K1 + 250.000 | 10.911 | 0°5'32.0'' | 0.004836 | 10.911 | 10.911 | 0.018 | 1 098 870.758 | 1 096 874.712 |
| K1 + 240.000 | 0.911 | 0°0'2.0'' | 0.000034 | 0.911 | 0.911 | 0.000 | 1 098 879.309 | 1 096 869.529 |
| TE K1 + 239.089 | 0.000 | 0°0'0.0'' | 0.00000 | 0.000 | 0.000 | 0.000 | 1 098 880.088 | 1 096 869.055 |
Fuente: Vargas Vargas, Gonzalez Vergara & Rincon Villalba (2013)
