Elementos de la espiral

Los elementos de la espiral así como su nomenclatura se presentan a contunuación y su determinación matemática y geométrica es la siguiente:

Parámetro “A”

Figura 1. Elementos de la espiral

La espiral se define como una curva tal que su radio es inversamente proporcional a su longitud, es decir que, en una espiral el producto de su radio con la longitud siempre será el mismo, independiente del punto que se analice sobre la espiral, la raíz cuadrada de este producto recibe el nombre de parámetro y su ecuación intrínseca es:

o

Donde:

L = Longitud desde el origen a cualquier punto p, (m)

R = Radio en cualquier punto p, (m)

A = Parámetro de la clotoide, (m)

Le = Longitud de la espiral (m)

Rc = Radio del círculo o de la espiral (m)

Como se observa en la figura en el punto de inflexión de la espiral (origen del sistema cartesiano), el radio de curvatura es infinito y la longitud de espiral es nula (R = ∞, L = 0), este punto será el punto de inicio de la rama de espiral que se utilizará para el diseño vial y se hará coincidir con el elemento en tangente (recta) tanto de entrada como de salida (TE o ET).

Como se establece más adelante existe un rango de valores apropiados para determinar el parámetro de la espiral, por lo tanto, para cada solución con base en el radio de curvatura establecido, existen varios valores de parámetros o familias de espirales a ser utilizadas. Las espirales de parámetro A grande, aumentan lentamente su curvatura y, por consiguiente, son aptas para la marcha rápida de los vehículos. Las espirales de parámetro A pequeño aumentan rápidamente su curvatura por lo que se recomiendan para velocidades bajas.

El parámetro, al establecer el tamaño de la espiral, fija la relación entre R (radio), L (longitud) y O (ángulo de giro de la espiral).

Ángulo de giro de la espiral “Oe”

Ángulo conformado entre el alineamiento que pasa por el origen de la espiral (TE o ET) y la línea tangente a la espiral en su punto de longitud máxima (EC o CE).

Figura 2. Ángulo de giro

Sí

entonces

De la figura 2:

θ_e expresado en radianes.

Ecuaciones paramétricas “X, Y”

Corresponde al valor de la abscisa (X) y la normal a la tangente (Y) que determinan la ubicación de cada punto de la espiral con respecto al alineamiento sobre el cual se encuentra el origen de la rama de espiral.

De la figura anterior se obtiene

Por series:

Por tanto, para x se tiene:

De (2) sabemos que

, remplazando se tiene

Recordando (2) sabemos que

, remplazando se tiene

Para y se tendrá:

De (2) sabemos que

, remplazando se tiene

Recordando (2) sabemos que

, remplazando se tiene

X y Y, son las ecuaciones paramétricas de la espiral.

De manera similar las coordenadas (x_p,y_p) en cualquier punto (p) de la espiral están dadas por:

Donde θ en radianes, y

El cálculo de X y de Y se puede obtener por computadores (u ordenadores) o en calculadoras programables o mediante tablas que requieren interpolar valores.

La siguiente figura, presenta la ubicación de X, x_p, Y y y_p, donde p es un punto cualquiera de la espiral.

Figura 3. Ubicación de X, x_p, Y y y_p

Longitud de la curva espiral “L_e”

De la ecuación se obtiene:

o,

θe en radianes.

Disloque de la espiral “ΔR”

Es la distancia a la que se desplaza el círculo de radio Rc respecto de los alineamientos, en la figura 21 se observa que el disloque es la distancia rs, y con base en este segmento, la distancia Y y el triángulo rectángulo oqp, se establece que:

Longitud de abscisa media “X_M”

Es la distancia medida entre el origen de la espiral y la proyección perpendicular sobre el alineamiento del origen desplazado del círculo. En la figura 22, se observa que la abscisa media X_M es igual al valor de X menos el segmento pq del triángulo rectángulo oqp, por lo tanto:

Figura 4. Disloque ΔR

Figura 5. Abscisa media X_M

Longitud de la tangente larga “Tl”

Es la distancia medida entre el origen de la espiral y el PI auxiliar de la espiral, en el cual se forma el ángulo θ_e. En la Figura 6, se observa que la tangente larga Tl es igual al valor de X menos el segmento qs del triángulo rectángulo qps, por lo tanto:

Figura 6. Tangente larga Tl y Tangente corta Tc

Longitud de la tangente corta “T_c”

Es la distancia medida entre el PI auxiliar de la espiral y punto final de la espiral. En la Figura 6, se observa que la tangente corta T_c es igual al segmento ps del triángulo rectángulo qps, por lo tanto:

Longitud de la tangente del sistema de empalme “T_e”

Es la distancia medida entre el origen de la espiral y el PI del empalme. En la Figura 7, se observa que la tangente del empalme T_e es igual al valor de X_M más el segmento qv del triángulo rectángulo oqv, por lo tanto:

Longitud de la externa o bisectriz del sistema de empalme “E_e”

Es la distancia medida entre el PI del empalme y el punto medio del segmento circular. En la Figura 7, con base en el radio del empalme R_c y el triángulo rectángulo oqv, se determina el valor de E_e es igual a:

Figura 7. Tangente y espiral del empalme T_e y E_e

Ángulo de la cuerda larga de la espiral “ϕe”

Es el ángulo barrido entre la visual al PI del empalme y el punto final de la espiral, haciendo centro en el punto de origen de ésta, corresponde a la última deflexión o deflexión máxima de la espiral. En la Figura 8, se observa en el triángulo rectángulo rqs, que el ángulo ϕ_e esta dado por:

Figura 8. Cuerda larga Cle y deflexión de la espiral ϕ_e

Cuerda de la espiral “CLe”

Es la distancia medida entre los puntos de origen y final de la rama de espiral. En la Figura 8, con base en el triángulo rectángulo rqs, se determina el valor de CLe es igual a:

Deflexiones de la espiral

Generalizando las ecuaciones para cualquier punto pi> ubicado sobre la espiral se puede determinar el ángulo de deflexión de ϕ_p y la cuerda larga del punto - CLp:

Los valores de x_p y y_p se determinan con las ecuaciones para x y y.

Las deflexiones se miden sobre los puntos de origen de la espiral (TE o ET)

Para un adecuado diseño bajo parámetros de comodidad y seguridad es necesario garantizar que el arco de espiral este dentro de unos valores límite que garanticen las condiciones geométricas y dinámicas de conducción aceptables, estos valores son:

• Longitud mínima del arco de espiral

  Para determinar el valor de longitud mínima de espiral se estudia y analizan tres criterios relacionados, con la comodidad y seguridad del usuario de la vía. El valor mínimo de longitud corresponderá al máximo obtenido con dichos criterios.

• Criterio I. Variación uniforme de la fuerza centrífuga (J) (No compensada por el peralte)

  Como el peralte un vehículo que transita por una curva se ve afectado por una fuerza centrífuga correlacionada con su peso, la velocidad y el radio de curvatura, este efecto es contrarrestado por la componente radial del peso del vehículo. De esta manera la fuerza centrífuga residual que actúa radialmente sobre el vehículo es:

  

  donde a_cr es la aceleración residual.

  y

  Remplazando

  

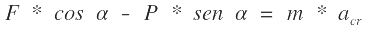
  dividiendo por cos α

  

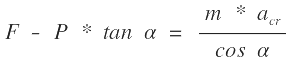
  Tan α = e. Para valores usuales de 8% se tiene un α máximo de 4°34’, por tanto cos α = 1

  

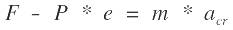
  remplazando los valores de F y P

  

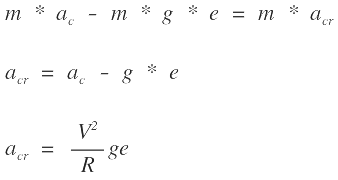
  El vehículo tarda un tiempo t en recorrer toda la longitud de transición Le a una velocidad uniforme V, llamemos J la variación de aceleración radial por unidad de tiempo, en el punto EC y se tendrá:

  

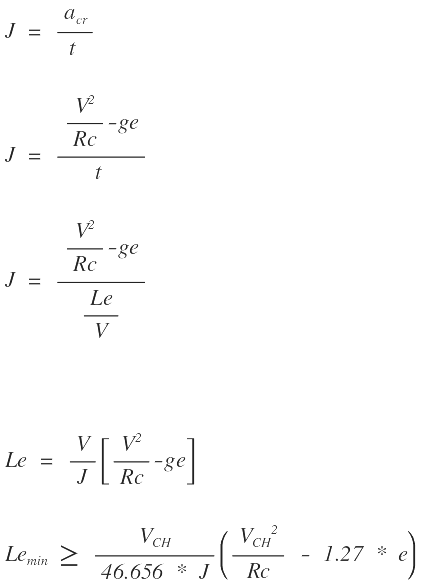
  Donde:

  Le_min: Longitud mínima, (m)

  V_CH: Velocidad específica, (km/h)

  Rc: Radio de cálculo de la clotoide, (m).

  J: Variación de la aceleración centrífuga, en m/s³

  e: peralte de la curva, (%).

  Utilizando la ecuación de A, obtenemos:

  

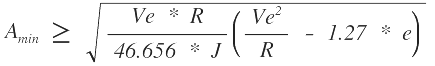
  Se adoptan para J, los siguientes valores:

  Tabla 1. Variación de la Aceleración Centrifuga

  Velocidad km/h	30	40	50	60	70	80	90	100	110	120	130	140	150
  J m/seg3	0.7	0.7	0.7	0.7	0.7	0.6	0.6	0.5	0.5	0.4	0.4	0.4	0.4

  Fuente: manual de Diseño Geométrico para Carreteras – INVIAS 2008

• Criterio II. Transición del peralte

  Para llevar la inclinación transversal de la calzada desde el bombeo natural “BN” hasta el valor del peralte “e” en la curva, se requiere una variación gradual en una longitud. Con base en lo establecido el peralte se tiene:

  

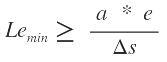
  Donde:

  Le_min: Longitud mínima, (m).

  R: Radio de Cálculo de la clotoide, (m).

  e: peralte de la curva, (%).

  a:Distancia del eje de giro al borde de la calzada, (m).

  Δs: Inclinación de la rampa de peraltes, (%).

  Utilizando la ecuación de A, obtenemos:

  

• Criterio III. Percepción y estética

  La longitud de la curva de la espiral ha de ser suficiente para que se perciba de forma clara el cambio de curvatura, originado alineamientos armoniosos y orientando al conductor sobre la trayectoria. Para ello, es necesario que se cumplan dos condiciones:

El disloque (ΔR) mínimo debe ser de 0.25 m.

Con base en la ecuación ΔR, se tiene

, y de las ecuaciones paramétricas se tiene:

Donde los valores de θ, el cos = 1 y el senθ = θ en radianes:

Para el punto máximo de y, se tiene:

Por otra parte

Pero como

Remplazando tememos que

Remplazando:

Donde:

Le_min: Longitud mínima, (m).

ΔR: Disloque de la clotoide, (m).

R: Radio de cálculo de la clotoide, (m).

Utilizando la ecuación de A, obtenemos:

El ángulo de giro de la espiral θe mínimo debe ser 3 grados

Donde:

Le_min: Longitud mínima, (m).

R: Radio de cálculo de la clotoide, (m).

θe: Angulo de giro de la espiral

Utilizando la ecuación de A, obtenemos:

Longitud máxima del arco de espiral

El valor de longitud máxima de espiral se establece como:

Donde:

Le_max: Longitud máxima, (m).

R: Radio de cálculo de la clotoide, (m).

Utilizando la ecuación de A, obtenemos: