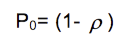Probabilidad de Poisson
La función de probabilidad de Poisson proporciona la probabilidad de x llegadas en un periodo específico. La función de probabilidad es:
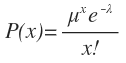
Para x = 0, 1, 2, ...
Las medidas de desempeño: el principal objetivo por el cual es importante el estudio de la teoría de colas consiste en poder dar respuesta a decisiones propias de la administración, pertenecientes al diseño y a la operación de un sistema de colas. Tomando nuevamente como ejemplo un banco, el gerente de dicho banco deberá decidir si programa tres o cuatro cajeros durante la hora de almuerzo. En una estructura de producción, el administrador puede desear evaluar el impacto de la compra de una nueva máquina que pueda procesar los productos con más rapidez.
En un modelo de una cola (M/M/1):(DG/∞/∞), las medidas de desempeño son
Factor de utilización de una cola (ρ)
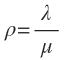
λ = Tasa media de llegadas. Es decir, es el promedio de clientes que ingresar al sistema en un tiempo determinado.
µ = La tasa media de servicio. Lo que indica es la capacidad de atención del o de los servidores del sistema.
Generalmente se requiere que ρ < 1, ya que si es mayor que uno, significa que el sistema está a punto de colapsar o ya colapsó, es decir, que si el factor de utilización es mayor que uno, no indica que en promedio llegan más clientes de los que son atendidos por el sistema.
Ls = Cantidad de clientes esperada en el sistema. Esta medida analiza el número de clientes en el sistema, incluyendo los clientes en la cola y los que son atendidos por el servidor.
Lq = Cantidad de clientes esperada en la cola. Esta medida busca analizar la longitud media de la cola del sistema, es decir, responde a la pregunta ¿cuántos clientes están esperando en la cola para ser atendidos?
Ws = Tiempo esperado en el sistema. Esta medida de desempeño busca dar respuesta a la siguiente pregunta: ¿Cuál es el tiempo que un cliente invierte en el sistema entero, incluyendo el tiempo de espera y el de servicio?
Wq = Tiempo esperado en la cola. Esta medida de desempeño busca dar respuesta a la siguiente pregunta: ¿Cuál es el tiempo promedio que un cliente recién llegado tiene que esperar en la fila antes de ser atendido?
Una vez definidas conceptualmente las medidas de desempeño de un sistema de línea de espera, se definirá matemáticamente dichas medidas para el modelo M/M/1:
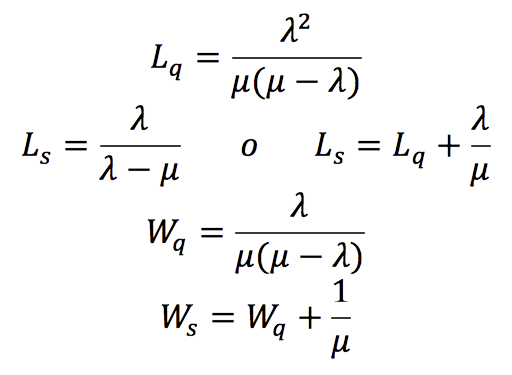
Además se tiene que:
Pn = Probabilidad de “n” clientes del sistema. Que busca contesta la pregunta ¿Qué tan probable es que haya n clientes en el sistema?, donde n=1, 2,3,…

P0 = Probabilidad de que no haya clientes en el sistema. Con esta probabilidad se analiza que tan probable es que en el sistema no haya ningún cliente: