Programación de proyectos con tiempos inciertos

A continuación se presenta un ejercicio de programación de proyectos con tiempos inciertos, tomado de: Bustos, E. Modelos de PERT/CPM probabilístico. México: Instituto Politécnico Nacional. Escuela superior de Cómputo. Recuperado de: https://bit.ly/2FVUbQN

Para incluir los tiempos inciertos de las actividades en el análisis de la red, es necesario obtener 3 estimaciones de tiempo para cada actividad. Las 3 estimaciones son:

• Tiempo optimista (a): el tiempo de actividad si todo marcha de manera ideal.
• Tiempo más probable (m): el tiempo con más probabilidad de una actividad en condiciones normales.
• Tiempo pesimista (b): el tiempo de actividad cuando se enfrentan demoras considerables.

Las 3 estimaciones de tiempo permiten al administrador desarrollar una mejor apreciación del tiempo más probable para la actividad, haciendo estimaciones de tiempos que varían desde el mejor tiempo posible hasta el peor.

Se puede determinar el promedio de tiempo de cada actividad mediante la siguiente fórmula.

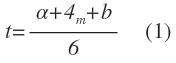
Con tiempos inciertos en las actividades, puede utilizarse la medida estadística común conocida como varianza para describir la dispersión o variabilidad en los valores de tiempo de una actividad. La varianza del tiempo de una actividad está dada por:

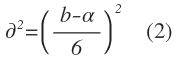
Como puede observarse, la diferencia entre la estimación pesimista y la optimista afecta en gran medida el valor de la varianza. Diferencias grandes en esos valores reflejan un elevado grado de incertidumbre en el tiempo de una actividad.

Las anteriores ecuaciones se basan en la suposición de que es posible describir la incertidumbre en los tiempos de actividad mediante una distribución beta de probabilidad. En la siguiente figura se presenta una distribución de probabilidad beta típica.

Variabilidad en el tiempo de terminación de un proyecto

Al realizar los cálculos de la ruta crítica, se consideró que eran fijos los tiempos de las actividades, e iguales a sus valores esperados; ahora es posible considerar la incertidumbre en los tiempos de actividad determinando el efecto de esta incertidumbre o variabilidad sobre el tiempo total que se requiere para terminar el proyecto. Recuerde que la ruta critica es: A – E – H – I – J y el tiempo esperado de terminación es de 17 semanas.

Al igual que las actividades de la ruta crítica gobiernan el tiempo total esperado de terminación del proyecto, la variación de las actividades en la ruta puede ocasionar variaciones en el tiempo total que se requiere para terminar el proyecto.

Por lo general, la variación en las actividades que no están en la ruta crítica no tiene efecto alguno sobre el tiempo total para la finalización del proyecto, debido al margen u holgura correspondiente a esas actividades. Sin embargo, si se prolongara una actividad no crítica lo suficiente para agotar todo su margen, entonces tal actividad se convertiría en parte de una ruta crítica y, cualquier demora adicional haría que aumentara el tiempo total necesario para terminar el proyecto. La variabilidad que conduce a un tiempo total mayor que lo esperado para las actividades de la ruta crítica, siempre hace que aumente el tiempo necesario para acabar el proyecto.

Por otro lado, la variabilidad en las actividades de la ruta crítica que da como resultado un camino crítico más corto, a menos que se vuelvan críticos los tiempos de las actividades en otras rutas. En seguida se utiliza la varianza en las actividades de la ruta crítica para determinar la varianza del tiempo de terminación del proyecto.

• E(T)= t_A + t_E + t_H + t_I + t_J
• E(T)= 6+3+4+2+2=17 Semanas

De manera similar, la varianza del tiempo total necesario para acabar el proyecto está dada por la suma de las varianzas de las actividades de la ruta crítica. Así que la varianza del tiempo de terminación del proyecto esta dada por:

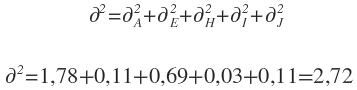
en donde 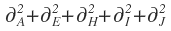son las varianzas de las actividades sobre la ruta crítica.

Esta fórmula se basa en la suposición en que todos los tiempos de las actividades son independientes. Si 2 o más actividades son dependientes, la fórmula sólo proporciona una aproximación de la varianza del tiempo de terminación del proyecto. Conforme más cerca estén las actividades de ser independientes, tanto mejor es la aproximación. Como se sabe que la desviación estándar es la raíz cuadrada de la varianza, puede calcularse la desviación estándar ∂ para el tiempo de terminación del proyecto puede calcularse de la siguiente manera:

Con esta distribución puede calcularse la probabilidad de cumplir con una fecha específica para la terminación del proyecto. Supóngase que los administradores han asignado 20 semanas para el proyecto del ejemplo. ¿Cuál es la probabilidad de que se cumpla con ese límite de 20 semanas? Utilizando la distribución normal se pide la probabilidad de que T ≤ 20.

El llamado valor z para la distribución normal en T = 20 está dado por:

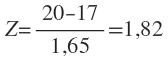
Utilizando z = 1,82 y la tabla de distribución normal, se observa que la probabilidad de que se satisfaga el límite de 20 semanas para el proyecto es 0,4656 + 0,5 = 0,9656. Es decir un 96,56% de que el proyecto se realice antes del límite de 20 semanas. Por ello, aunque la variabilidad en los tiempos de las actividades puede ocasionar que el tiempo total que se requiere para terminar un proyecto supere las 17 semanas, existe una excelente probabilidad de que el proyecto finalice antes del límite de 20 semanas.

Analice que sucede sí preguntan ¿Cuál es la probabilidad que el proyecto se realice antes de 15 semanas?

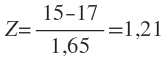
El signo menos significa que x = 15 está la izquierda de la media. Utilizando z = 1,21 y buscando en la tabla tenemos: 0,5 – 0,3869 = 0,1131, la probabilidad es muy baja, es decir existe un 11,31% que el proyecto se termine antes de 15 semanas.

¿Cuál es la probabilidad que el proyecto se realice en un tiempo superior a las 22 semanas? En este caso se tendría:

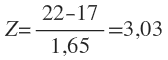
Buscando en la tabla se tiene y analizando la gráfica se tiene: P( T > 22) = 1 – P( T = 1 – 0,4988 = 0,5012). La probabilidad que el proyecto se realice por encima de 22 semanas es del 50,12%.