Formulación del modelo de transporte mediante programación lineal
Modelo de problema de transporte en su forma de tabla
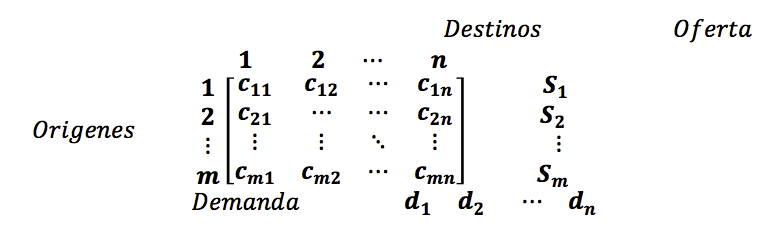
El problema de transporte formulado como un modelo de programación lineal
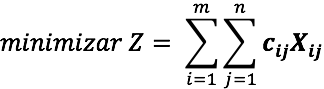
Sujeta a
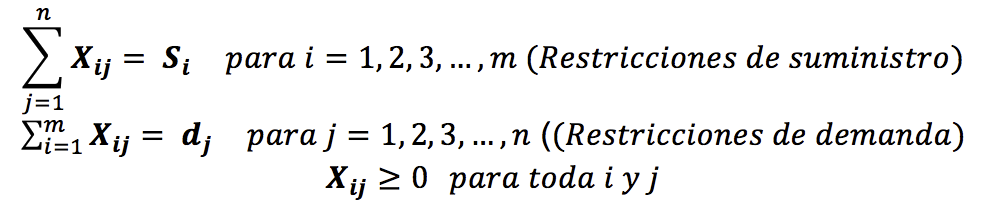
Notación:
- m = Número de puntos de suministro.
- n = Número de puntos de demanda.
- Xij = Cantidad de unidades enviadas desde punto de suministro i al punto de consumo j
- cij = costo unitario de enviar una unidad del punto de suministro i al punto de consumo j
- Si = Suministro en el punto i
- di = demanda en el punto j
Se considera que el modelo del problema de transporte se encuentra equilibrado (balanceado) si la sumatoria del suministro es igual a la sumatoria de la demanda. En caso de presentarse un desbalance se debe balancear un problema de transporte mediante adición de un punto de suministro ficticio o un punto de demanda ficticio.
Sean M centros de productores llamados orígenes y centros de consumo n denominados destinos. Sea "a" el número de unidades disponibles para ofrecerse en cada origen i (i=1,2,...., M) y sea b el número de unidades requeridas en el destino j (j= 1,2,..., N).
Sea Cij el costo de transporte por unidad en la ruta (i, j) que unen al origen i con el destino j. El objetivo es determinar el número de unidades transportadas del origen i al destino j de tal manera que se minimicen los costos totales de transporte.
Sean xij las cantidades a determinar
El problema de Programación Lineal asociado es:

El modelo de Programación lineal para dos orígenes, tres destinos:
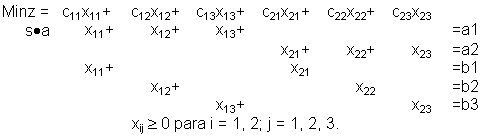
El modelo de programación lineal puede quedar como:
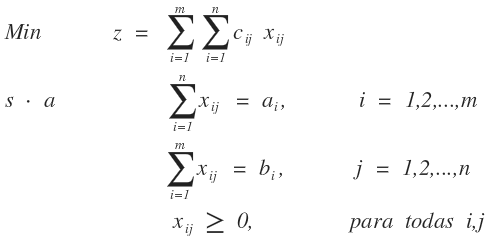
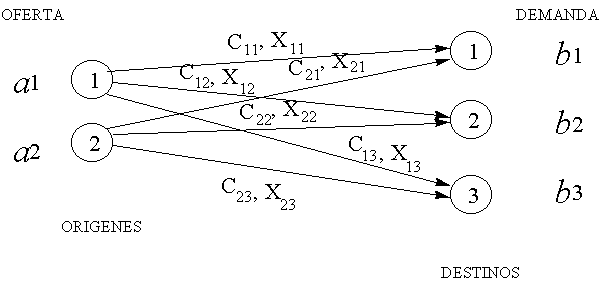
Figura 1. Representación gráfica dos orígenes, tres destinos
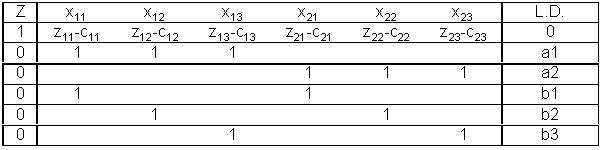
La siguiente tabla es una estructura simplex para dos orígenes, tres destinos: