Ejemplo 1E
Utilizar el método simplex para minimizar Z = x1 + 2x2 sujeta a
- 2x 1 + x 2 ≥ 1, ( 1 )
- x 1 + x 2 ≥ 2, ( 2 )
- x 1, x 2 ≥ 0.
Para minimizar Z, se puede maximizar -Z = -x1 -2x2. Obsérvese que las restricciones (1) y (2) tienen ambas la forma a1x1 + a2x2 ≥ b, en donde b ≥ 0. Por ello, sus ecuaciones implican dos variables de holgura s1 y s2, cada una de ellas con coeficiente -1, y dos variables artificiales t1 y t2.
- 2x1 + x2 - s1 + t1 =1, ( 3 )
- x1 + x2 - s2 + t2 = 2. ( 4 )
Como existen dos variables artificiales se maximiza la función objetivo W = (-Z) - Mt1 - Mt2, en donde M es el número positivo más grande. De forma equivalente,
x1 + 2x2 + Mt1 + Mt2 + W = 0.
La matriz de coeficientes aumentada de las ecuaciones (3) - (5) es
| x1 | x2 | s1 | s2 | t1 | t2 | W | |
| -2 | 1 | -1 | 0 | 1 | 0 | 0 | 1 |
| -1 | 1 | 0 | -1 | 0 | 1 | 0 | 2 |
| 1 | 2 | 0 | 0 | M | M | 1 | 0 |
Procediendo se obtienen las tablas I, II y III.
Tabla 1. Simplex I
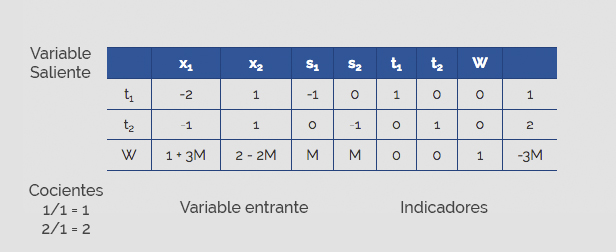
Tabla 2. Simplex II
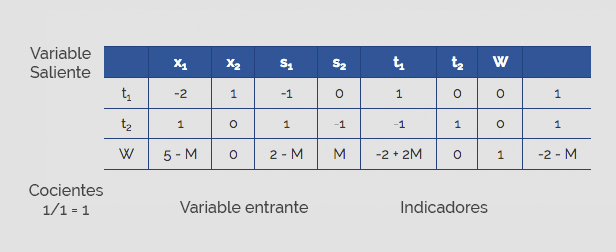
Tabla 3. Simplex III
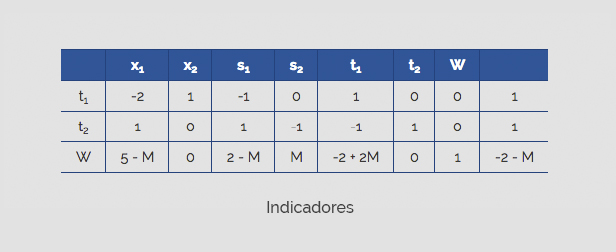
La S.F.B. que corresponde a la tabla III tiene ambas variables artificiales iguales a 0. Así, ya no se necesitan las columnas de t1 y t2. Sin embargo, los indicadores de las columnas de x1, x2, s1 y s2 son no negativos y, en consecuencia se ha llegado a la solución óptima. Dado que W = -Z cuando t1 = t2 = 0, el valor máximo de -Z es -4. Por lo tanto. el valor mínimo de Z es - (-4), o bien 4. Aparece cuando x1 = 0 y x2 = 2.
