

Se expresa de la siguiente manera:
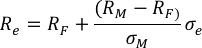
En donde:
Re: Rentabilidad esperada del portafolio eficiente
RF: Retorno esperado de activos libres de riesgo
RM: Retorno esperado de activos con riesgo
σM: Riesgo del mercado
σe: Riesgo del portafolio eficiente
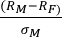 : Prima por unidad de riesgo, retorno adicional obtenido por riesgo
: Prima por unidad de riesgo, retorno adicional obtenido por riesgo
en donde el portafolio eficiente es aquel portafolio conformado por activos libres de riesgo y activos con riesgo. La ecuación del mercado de capitales está representado por la Línea del Mercado de Capitales (CML), por sus siglas en inglés (Capital Market Line), el retorno esperado de un portafolio eficiente es el retorno libre de riesgo más la prima por riesgo multiplicada por el nivel de riesgo asumido, modelo que se conoce con el nombre de Modelo de Fijación de Precios de Activos d Capital (CAPM).
Rp= (1/2)(0,10)+(1/2)(0,05)= 0,075
σp=(1/2)(0,06)+(1/2)(0,00)= 0,03
Para un portafolio conformado por el 50% de los fondos invertidos en activos con riesgo y el 50% de los fondos invertidos en activos libres de riesgo. Este resultado muestra que el riesgo de los activos con riesgo ha sido reducido de 0,06 a 0,03, simplemente incluyendo activos con riesgo, pero que la rentabilidad esperada también se ha reducido de 0,10 a 0,075 y aplicando la ecuación desarrollada.
Igualmente el participante puede verificar que si puede obtener fondos a tasa libre de riesgo y colocarlos en activos con riesgo (inversiones apalancadas); por ejemplo, prestar el 25% a tasa libre de riesgo y colocar los fondos totales en activos con riesgo, se obtendría el siguiente resultado:
Rp= (1,25)(0,10)+(-0,25)(0,05)= 0,1125
σp= (1,25)(0,06)+(-0,25)(0,00)= 0,075
Que evidentemente es portafolio con un retorno esperado superior al retorno de los activos con riesgo, por supuesto también con su correspondiente incremento de riesgo.
Aplicando la ecuación de la línea de mercado de capitales, se obtienen los siguientes resultados:
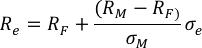
Reemplazando los valores correspondientes se tiene:
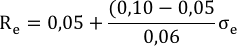
La ecuación de la línea de mercado de capitales para este caso es:
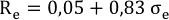
En donde la prima por riesgo es de 0,833.