Ejemplo

Para el retorno esperado del portafolio en el caso de tres valores, la expresión es la misma que para el caso de dos valores:

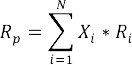
   Donde:

           R_p : Retorno esperado del portafolio

           X_i : proporción del total del portafolio invertido en i  

           R_i : Retorno esperado de la i-ésima acción

           N: Número total de acciones en el portafolio, para el cual N=3

Para el riesgo del portafolio se requiere conocer la desviación estándar de los valores componentes del portafolio, los coeficientes de correlación de las combinaciones de los valores A,B,C, así como las proporciones de monto invertido en cada una de las acciones del portafolio, la desviación estándar o en otras palabras el riesgo del portafolio de tres valores puede obtenerse con la siguiente expresión.

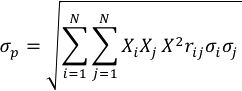
    Donde:          

           σ_p: Riesgo del portafolio (desviación estándar)
           X_i: porcentaje del portafolio invertido en la acción X
           X_j: porcentaje del portafolio invertido en la acción y
           σ_i: Riesgo de la acción i (desviación estándar de i)
           σ_j: Riesgo de la acción j (desviación estándar de j)
           r_ij: coeficiente de correlación entre i y j
           N: Numero de acciones del portafolio

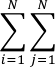: Doble sumatoria para ser tomados juntos cada número es obtenido sustituyendo las parejas i, j dentro de la expresión.

Si usamos la ecuación de riesgo del portafolio para dos valores y expandimos para tres valores, (N=3), tenemos la siguiente expresión para el riesgo de un portafolio de tres valores:

Tómese como ejemplo el participante puede calcular fácilmente, el retorno esperado y el riesgo del portafolio para tres acciones con las siguientes características:

El retorno esperado del portafolio será:

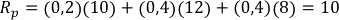
Y el riesgo del portafolio será:

                      
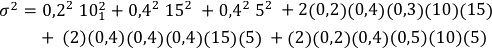
es decir

                       σ²= 4+36+4+7,2+9,6+4=64,8
σ=8

estos resultado son para un portafolio de 3 valores.