

El riego de la acción Y es más alto que el de la acción X. Es cierto que X y Y tienen el mismo retorno esperado, calculado con los retornos y probabilidades mencionadas en la tabla, obsérvese que cuando el retorno esperado de X es alto el de Y es bajo y viceversa. La pregunta clave: ¿es el portafolio compuesto por algún monto invertido en X y otro invertido en Y, superior a las acciones individuales?, ¿tienen menor nivel de riesgo?. A continuación se indica cómo construir un portafolio para dos acciones:
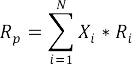
Donde:
Rp: Retorno esperado del portafolio.
Xi: Proporción del total del portafolio invertido en i.
Ri : Retorno esperado de la i-ésima acción.
N : Número total de acciones en el portafolio.
En resumen, puede encontrarse dos valores en cuyo comportamiento tengan una correlación inversa; es decir, cuando un título tiene un retorno esperado alto, el otro tiene un retorno esperado bajo. Esta correlación puede encontrarse con la siguiente expresión:
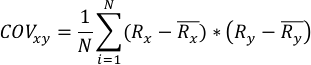
Donde:
COVxy: Covarianza entre X y Y.
Rx : Retorno de la acción X.
Ry : Retorno de la acción Y.
Rx : Retorno esperado de la acción X.
Ry : Retorno esperado de la acción Y.
N : Número de observaciones.
El coeficiente de correlación es otra expresión de las diferencias de comportamiento ente X y Y , que puede definirse con la siguiente expresión:
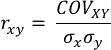
Donde:
rxy: Coeficiente de correlación entre X y Y.
αx : Desviación estándar de X.
αy : Desviación estándar de Y.
Dicho coeficiente puede variar entre ± 1, nótese que el efecto de cartera está íntimamente relacionado con el coeficiente de correlación. En el sentido que entre menor sea el coeficiente de correlación en términos absolutos mayor será el efecto de portafolio. Lo anterior significa que si el coeficiente de correlación es 1 el efecto de portafolio es nulo y las dos acciones no se podrán combinar de ninguna manera para encontrar un portafolio con riesgos más bajos que sus componentes. Si es -1, el efecto de portafolio es máximo. Es factible combinar dos acciones de tal forma que se puede obtener riesgo menor. En el ejemplo presentado, el participante puede calcular fácilmente que el coeficiente de correlación es de rxy=-1. Esta es una correlación perfecta negativa y por lo tanto la reducción del riesgo del portafolio es máxima; es decir, se obtiene el máximo efecto de portafolio. Para completar este tema, se presenta a continuación la expresión que permite calcular el riesgo del portafolio de dos valores:
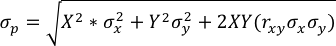
Donde:
αp: Riesgo del portafolio (desviación estándar.
X : Porcentaje del portafolio invertido en la acción X.
Y : Porcentaje del portafolio invertido en la acción Y.
αx : Riesgo de la acción X (desviación estándar de X).
αy : Riesgo de la acción Y (desviación estándar de Y).
rxy: Coeficiente de correlación entre X y Y.