

Los sistemas de ecuaciones que forman un sistema lineal de dos ecuaciones con dos incógnitas son funciones de primer grado, es decir rectas. El método gráfico consiste, en representar en un plano cartesiano, ambas rectas y comprobar si se cortan o no. Debe tenerse en cuenta, que, en el plano, dos rectas sólo pueden tener tres posiciones relativas (entre sí): se cortan en un punto, son paralelas o son coincidentes (la misma recta). Si las ecuaciones se cortan en un punto, las coordenadas de éste (x, y) conforman la única solución del sistema, ya que son los únicos valores de ambas incógnitas que satisfacen las dos ecuaciones del sistema, y se dice que es compatible determinado. Si las rectas son paralelas, no habrá puntos en común, por lo que no habría ningún par de números que representen el corte de ambas rectas, es decir, que satisfaga las solución de los dos sistemas a la vez, por lo que éste será incompatible, o sea sin solución. Por último, si ambas rectas están una sobre la otra, hay infinitos puntos que pertenecen a ambas, lo cual nos indica que hay infinitas soluciones del sistema, luego éste será compatible indeterminado.
Entre María y Juan tienen 600 usd, pero Juan tiene el doble de usd que María. ¿Cuántos uds tiene cada uno?.
Si x es la cantidad de usd de María e y el de Juan. Se puede expresar las condiciones del problema mediante ecuaciones: Si los dos tienen 600 usd, esto da la ecuación x + y = 600. Si Juan tiene el doble de usd que María, su ecuación es y = 2x. Ambas ecuaciones forman el siguiente sistema:
x + y = 600
2x - y = 0
Para resolver el sistema por el método gráfico se despeja la variable y en ambas ecuaciones y se tendrá:
y = -x+600
y = 2x
Ahora, se puede representar ambas rectas, y su tabla de valores:
| y = -x + 600 | y = 2x | ||
| x | y | x | y |
| 200 | 400 | 100 | 200 |
| 600 | 0 | 200 | 400 |
Con estas tablas de valores para las dos rectas y eligiendo las escalas apropiadas en los ejes OX y OY, se representan gráficamente:
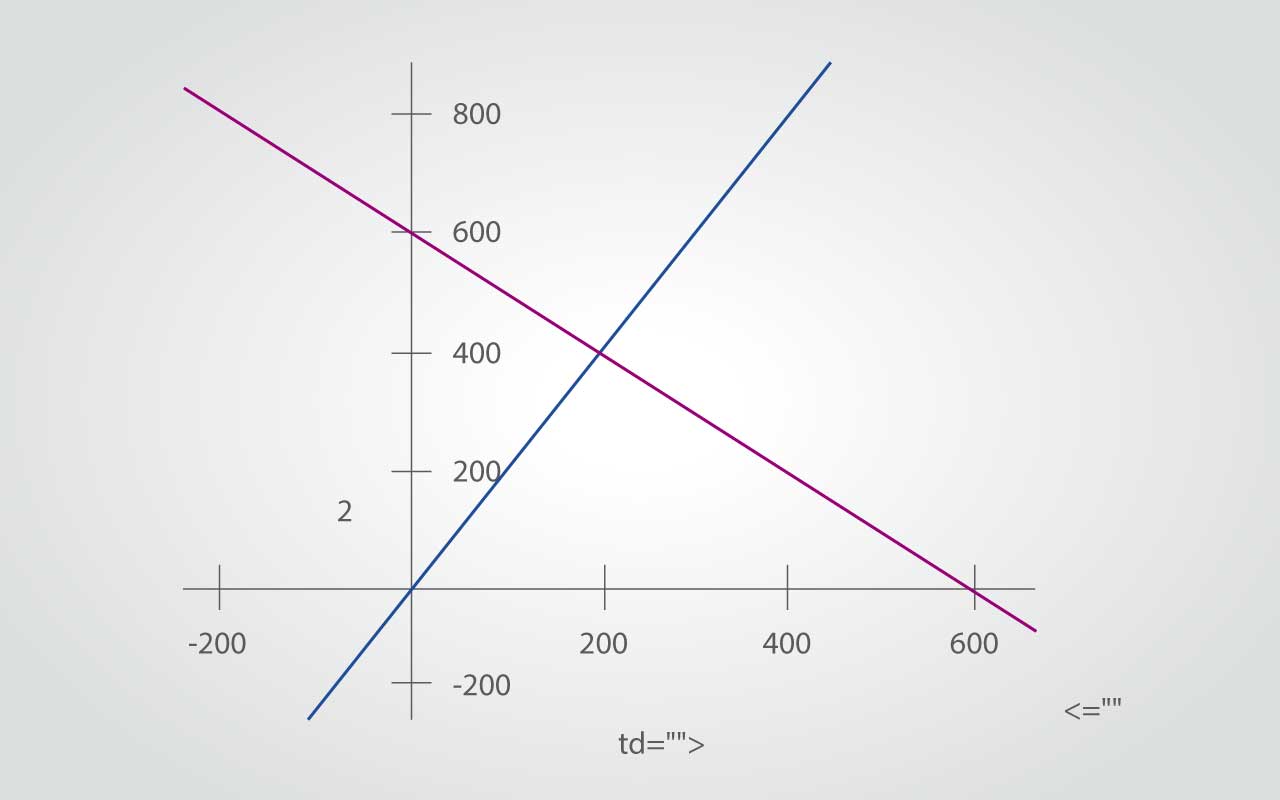
Se puede ver claramente que las dos rectas se cortan en el punto (200, 400), luego la solución del sistema es x = 200 e y = 400. Por tanto, la respuesta al problema planteado es que María tiene 200 usd y Juan tiene 400 usd.